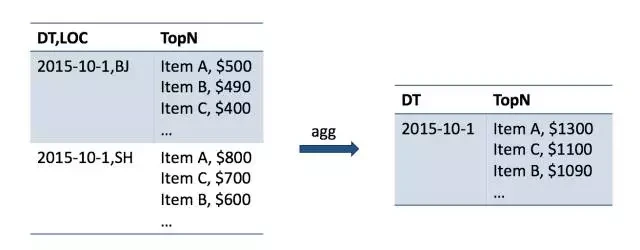
Apache Kylin 是一个开源的分布式分析引擎,提供 Hadoop 之上的 SQL 查询接口及多维分析(OLAP)能力以支持超大规模数据。它能在亚秒内查询巨大的数据集 。本文将详细介绍 Apache Kylin 1.5 中的新功能: Top-N 预计算。
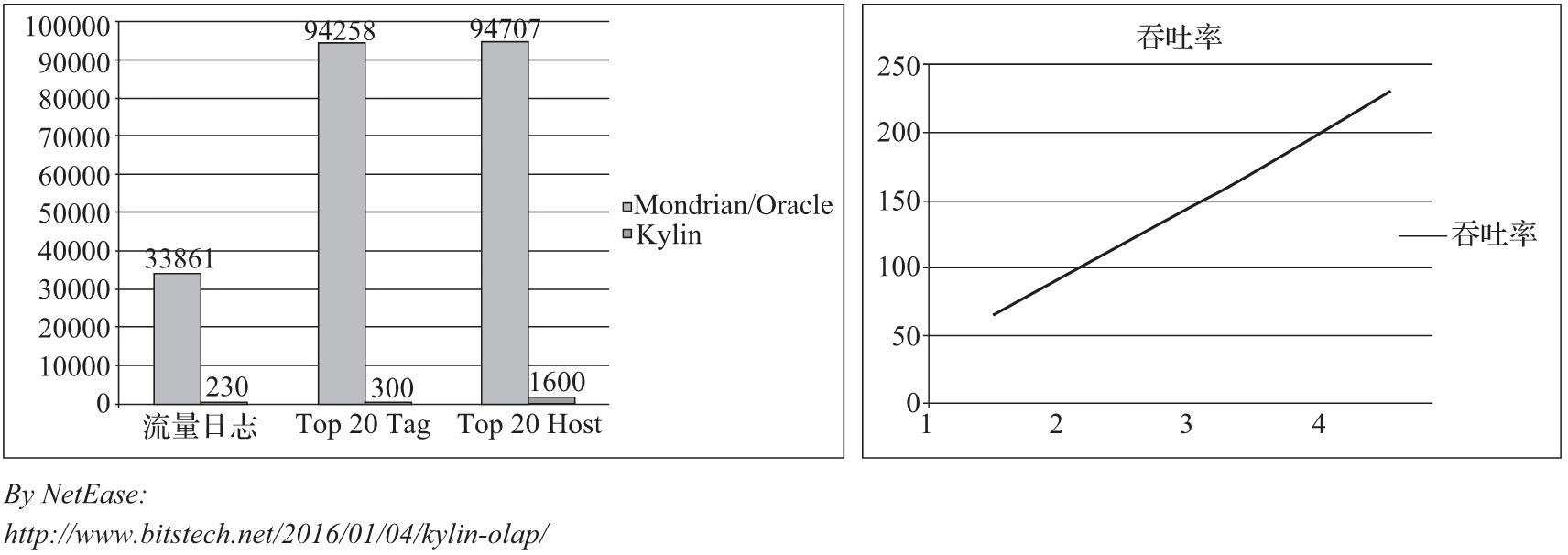
大家都听过二八定律,这是在很多领域存在的规律,例如世界上 20% 的人占有了超过 80% 的财富;20% 最受欢迎的商品,贡献超过了 80% 的销售额等等。 二八定律背后的规律是 Zipf 分布法则,它是美国学者 G.K. 齐普夫在统计英文单词出现频率时发现的规律。简单说就是如果把频率出现最高的单词的频率看作是 1 的话,第二个出现的频率是二分之一,第三个是三分之一,依此类推,出现的频率是它排名的某次幂分之一。
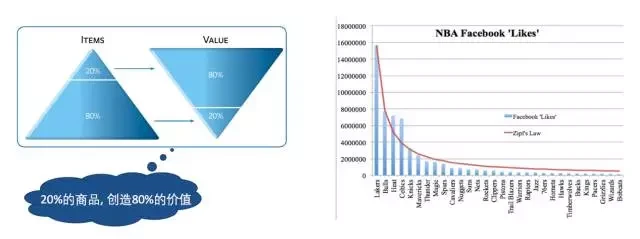
图 1 二八原则和 Zipf 分布
图 1 的右图是 facebook 上统计的 NBA 各球队受赞次数排名,它也基本符合 Zipf 分布。
在互联网时代,还有一个知名的理论-长尾效应,举例来说就是某个网站的用户或者商品的数量非常的多,但是大部分都是访问频率(或价值)极低的,这条尾巴可以很长。长尾的存在对大数据分析带来挑战,因为它的基数(cardinality)特别高,如何从中快速找到高价值的商品或者用户,是一个迫切而难度很高的任务。
图 2 长尾
现在来看一个典型的 Top-N 查询示例。该查询是选择在 2015 年 10 月 1 日,地址在北京,销售商品按价格之和排序(倒序),找前 100 个。

在 Kylin v1.5 之前,SQL 中的 group by 列,需声明成维度,所以这个 Cube 的维度中要有日期,地点和商品名,度量是 SUM(PRICE) 。图 3 展示了一个这样设计 Cube。因为商品的基数很大,计算的 cuboid 的行数会很多;而度量值 SUM(PRICE) 是非排序的,因此需要将这些纪录都从存储器读到 Kylin 查询引擎中(内存), 然后再排序找出最高的纪录;这样的解决办法总 开销较大 。
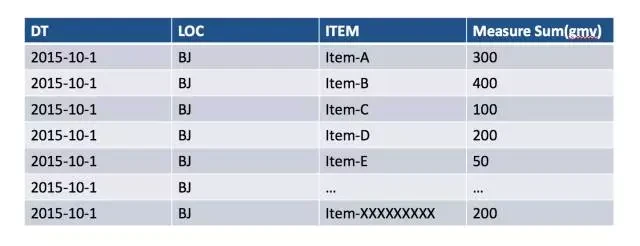
图 3 用普通度量处理 Top N 查询
针对上面的情形,Kylin 开发团队决定 另辟蹊径 来处理这种查询,研究了多种 Top-N 的解决方法;由于在大数据的背景下,算法要求一定是可并发执行的,计算结果是需要可再次合并的,而计算结果的少量误差是可以接受的; 最终 Kylin 选择了 Space-Saving 算法 [1],以及它的一个衍生版 Parallel Space-Saving[2],并在此之上做了特定的优化。这种算法的优势是使用较少的空间,同时保证较高的精确度。
有了 Top-N 之后,Cube 的设计会比以前简单很多,因为像刚才的商品名会被挪到 Measure 中去,在 Measure 里按 Sum 值做倒序,只保留最大的若干值。
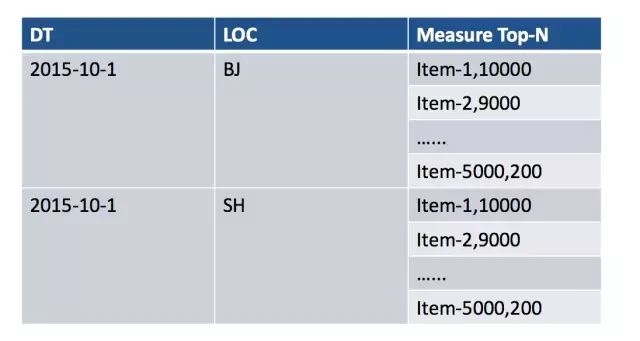
图 4 使用 Top N 度量的 Cube
值得一提的是需要用多少空间运算 Top-N 。简单来说存储空间越多准确率越高。我们通过使用生成一些样本数据然后用 Space-Saving 计算,并且跟真实结果做比较,发现 50 倍空间对于普通的数据分布是够用的。也即,用户需要 Top 100 的结果,Kylin 对于每种组合条件值,保留 Top 5000 的纪录, 并供以后再次合并。这样即使多次合并, Top100 依然是比较接近真实结果 。

图 5 Top N 度量的合并
Top-N 的优点:因为它只保留 Top 的记录,会让 Cube 空间大幅度减少,而查询性能大大提升。在一个典型的例子里,改用 Top-N 后,Cube 的大小减少了 90%,而查询时间则只有以前的 10% 不到。
缺点 是它可能是近似的结果(当 50 倍空间也无法容纳所有基数的时候)。如果业务场景需要绝对精确的话,它可能不适合。
Top-N 误差率由很多因素决定的 :
未来 Top N 的功能将有了进一步提升,例如可以将多个维度放入到 Top N 度量中,使用非字典编码等,敬请期待。
[1] Ahmed Metwally, et al. “Efficient computation of frequent and top-k elements in target="_blank">杜小芳对本文的审校。
给InfoQ 中文站投稿或者参与内容翻译工作,请邮件至editors@cn.infoq.com。也欢迎大家通过新浪微博(,@丁晓昀),微信(微信号:InfoQChina)关注我们。