什么是 LLM 推理?
LLM 推理指的是模型的这些能力:
尽管大语言模型并没有专门被训练用于执行推理任务,但它们有时候表现出类似推理的能力。
为什么 LLM 推理很重要?
LLM 推理能力之所以重要,有这几个原因:
当 OpenAI 推出 O1 和 O1-mini 时,我意识到,如果 AI 能够通过深入思考来解决更复杂的问题,这将是向人工通用智能(AGI)迈出的一大步,也是利用 AI 解决复杂问题的创新。后来,我突发奇想:如果我们能够提升当前顶尖模型——比如 Claude Sonnet 3.5——的推理能力,使其达到甚至超越 O1 模型的水平,那将会怎样呢?
在阅读了一些资料,如东北大学的“反思”论文和 reddit 上的一些评论后,我决定创建一种新的提示词范式,结合动态思维链 + 反思 + 口头强化,尝试将其作为一个实验来付诸实践。
编码和解决数学问题的提示词示例:
提示词范式解释
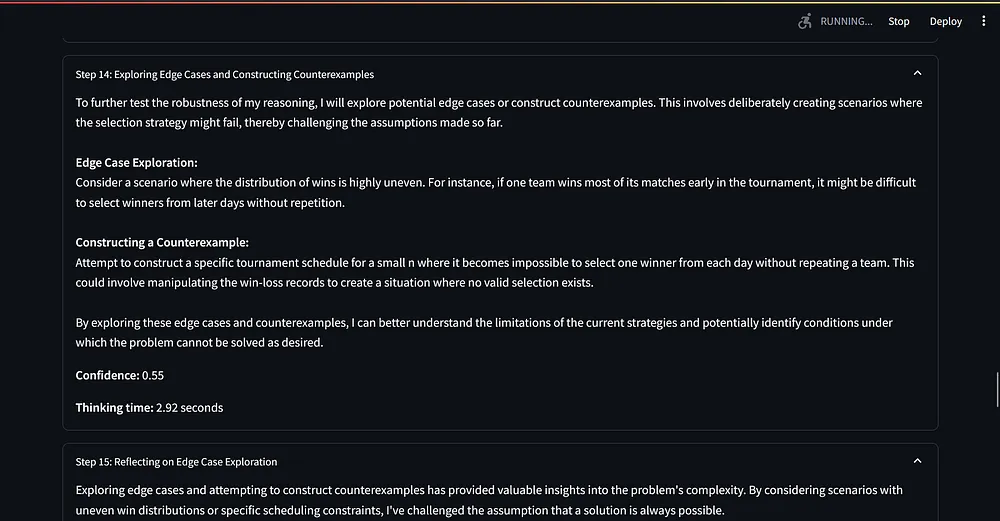
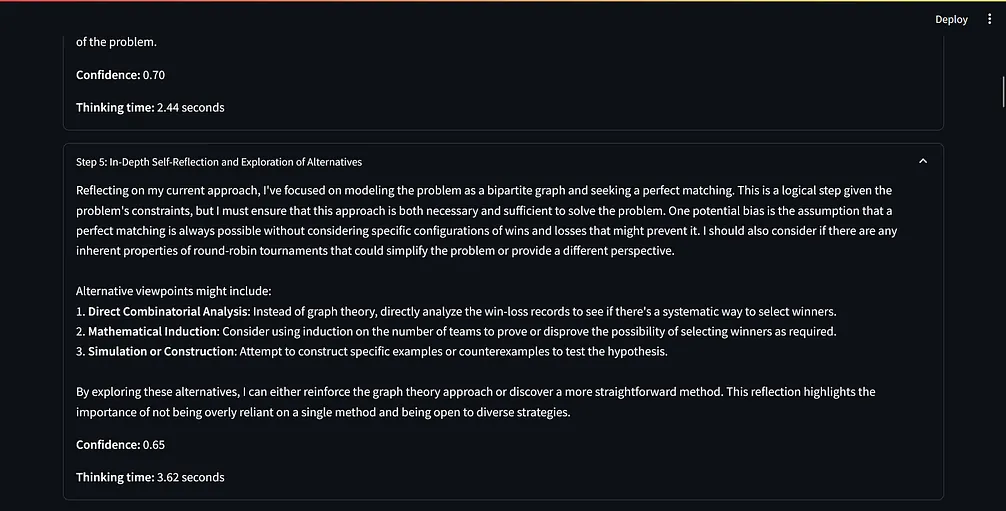
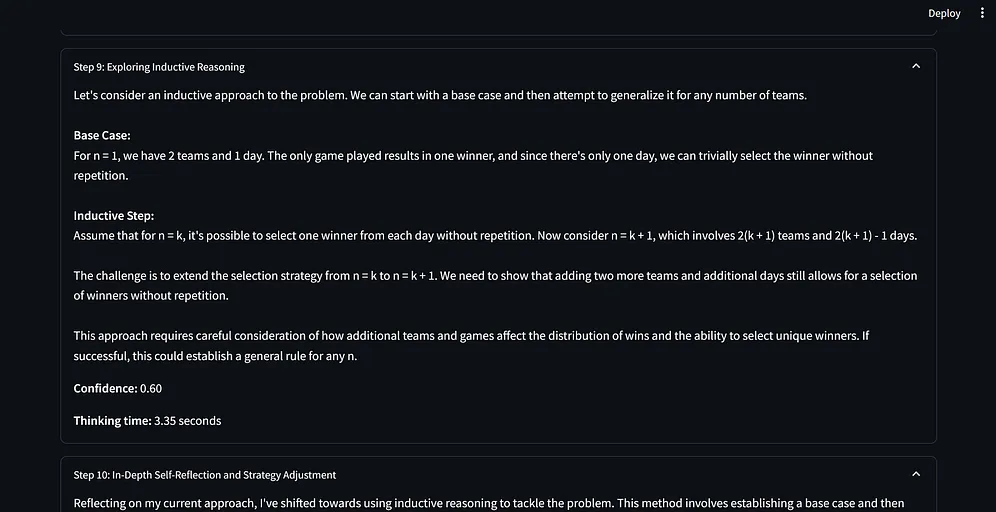
动态思维链、反思和口头强化学习相结合,创建了一个具有高度适应性和响应性的问题解决系统。这个过程从思维链生成初始推理路径开始,然后通过反思机制进行评估和完善。在每个反思阶段之后,模型以奖励分数(用于指导未来的推理步骤)的形式接收口头强化。
这个循环过程使得模型能够不断优化输出,适应不断变化的条件,并有效应对复杂的场景。例如,在涉及多阶段决策的复杂任务中,如自动驾驶导航,模型可能会首先采用动态思维链来探索可能的行动路径。
在遇到障碍或环境发生变化时,反思机制使其能够重新评估并调整策略,而口头强化分数则提供了具体的行动调整指导。这就有了一个能够从经验中持续学习并不断进步的 AI 系统,随着时间的推移,其推理能力得到显著提升,在应对动态变化的真实世界问题时展现出更加强大的问题解决技能。
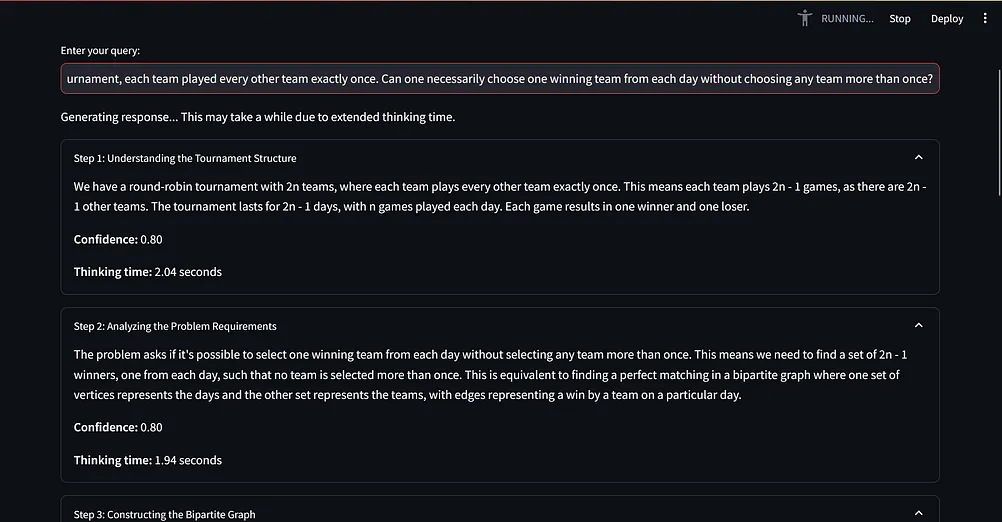
提示词范式的基准测试
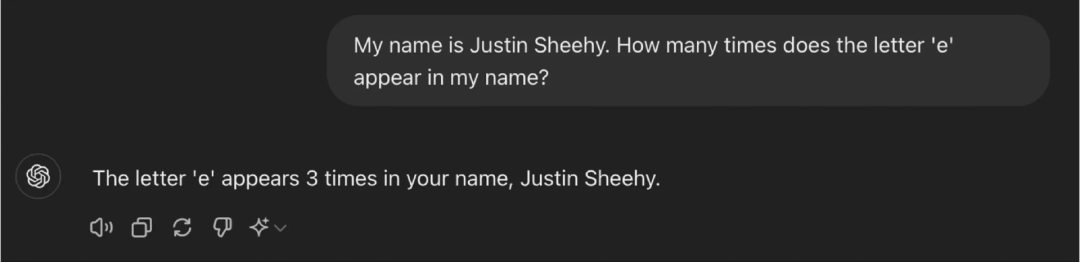
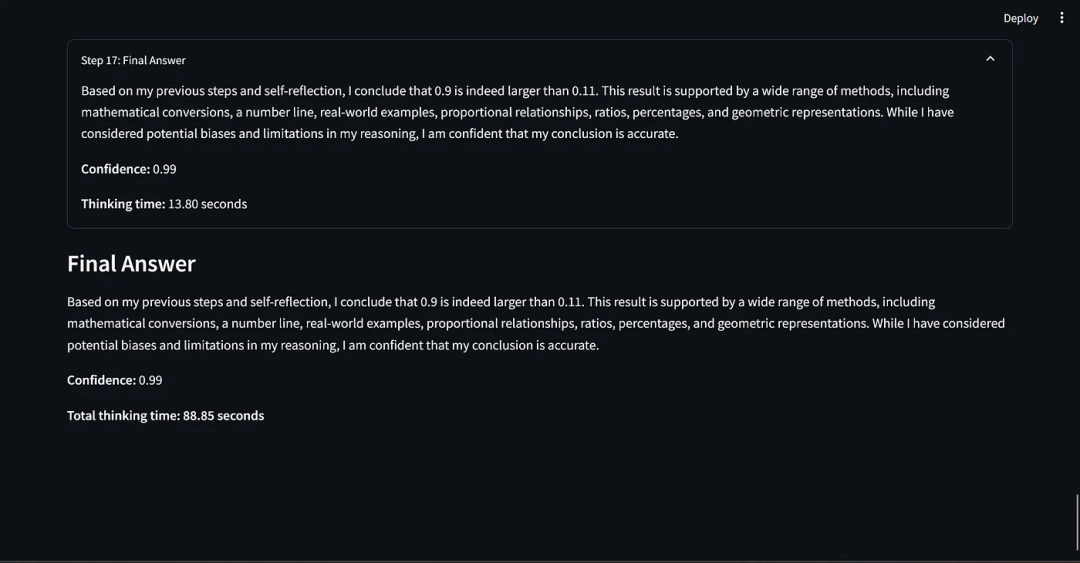
我想知道这个提示词范式的有效性,尽管已经能够回答经典的问题,如“计算单词 strawberry 中 r 的个数”和“比较 0.9 和 0.11 哪个更大”等。
据我所知,只有 O1 和 O1 mini 能够全部回答正确,得益于它们内部的推理机制。
我为基准测试创建了两组数据集。
第一组数据集来自 JEE Advanced(联合入学考试)和 UPSC(印度公务员考试)预选考试。
JEE Advanced 被认为是全球最难的本科入学考试之一,专为那些有志于进入印度最顶尖学府——印度理工学院的学生而设。
UPSC 公务员考试被誉为全球竞争最激烈的考试之一,吸引了众多希望在印度政府机构中担任行政职务的考生。其综合性的通识测试覆盖了广泛的知识领域,可以作为对大语言模型进行严格和全面评估的有效工具。
这些问题设计得非常严格,旨在深入考察考生的概念理解、问题解决能力,以及在物理、数学、化学、社会科学等多个领域应用知识的能力。
用于评估的工具和脚本:
我修改了 Benjamin Klieger 的脚本,其原始版本在这里:。
为了实现这些逻辑,我对原始版本进行了修改。用户向 AI 系统提出一个问题,系统需要提供足够的时间从多种角度思考问题,并最终给出解决方案。在这一过程中,我尝试模仿人类解决复杂问题时的思考方式,将其应用于 AI 系统中。这一灵感来源于 Aravind Srinivas 在接受 Lex Fridman 采访时所分享的观点。
基准测试结果分析
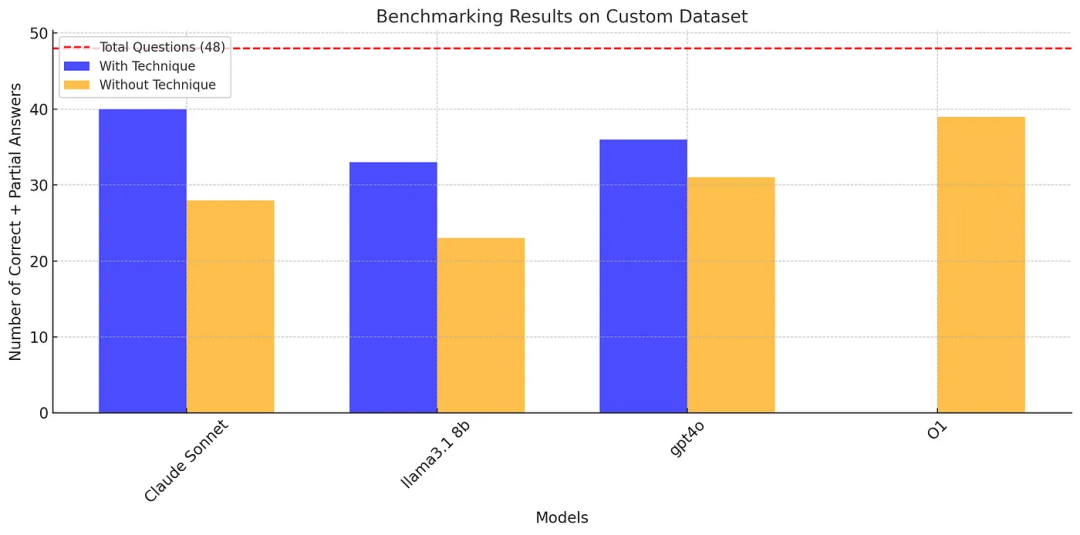
结果表明,应用动态思维链、反思和口头强化学习技术显著提升了大多数模型的性能,特别是 Claude Sonnet 和 Llama 3.1 8b。
A. 应用了这个范式的 Claude Sonnet 获得了最高分(40/48),在数学、物理和化学问题上表现出色。Llama 3.1 8b(33/48)和 GPT-4O(36/48)的表现在应用了这个范式后也得到了显著改进。
B. 在没有应用这个范式的情况下,除了 O1,所有模型的表现都有所下降。值得注意的是,O1 在没有应用任何范式的情况下得分为 39/48,表明其具有强大的固有问题解决能力。
可以看出,Claude Sonnet 3.5 有能力超越 O1。
这个基准测试有点宽松,即对于部分正确的答案也给了分数。
注意:在进行这次基准测试时,Meta 还没有发布 llama 3.2。
OpenAI 声称 O1 在国际数学奥林匹克问题上能够获得 83% 的分数。使用我们的提示词范式,Claude Sonnet 在第一次尝试中能够获得 50% 的分数,如果多次尝试,Claude Sonnet 3.5 有可能会超越 O1。



针对 Putnam 数据集的基准测试
什么是 Putnam 数学竞赛?
William Lowell Putnam 数学竞赛,通常被称为 Putnam 竞赛,是美国和加拿大本科生极具挑战性的数学竞赛。以下是竞赛的关键点及其难度评级。
竞赛结构:
难度评级:
Putnam 竞赛被认为是全球最难的本科数学竞赛之一,其难度可以通过以下几个方面看出:
中位数分数:中位数分数通常为 0 或 1 分(满分 120 分)。这意味着超过一半的参与者要么完全解决不了问题,要么最多解决一个问题。
在竞赛的 85 年历史中,仅有五位参赛者荣获满分,这一事实突显了攻克所有竞赛题目的非凡挑战。
因此,如果以 1 至 10 的评分作为标准,10 代表最难,那么 Putnam 竞赛在本科数学竞赛中的难度评级应为 9 或 10。
我从 2013 年到 2023 年的 Putnam 竞赛试卷中挑选了大约 28 个问题。
基准测试结果分析
在这个基准测试中,llama3.1 70B、Claude Sonnet 和 o1 mini 解决了 14 个问题,而 O1 解决了 13 个问题,gpt4o 解决了 9 个问题。
乍一看,这个结果似乎好得令人难以置信!
我相信 gpt4o 表现不佳是因为它创建了 50 到 60 个推理链循环,最终给出了一些无意义的答案。
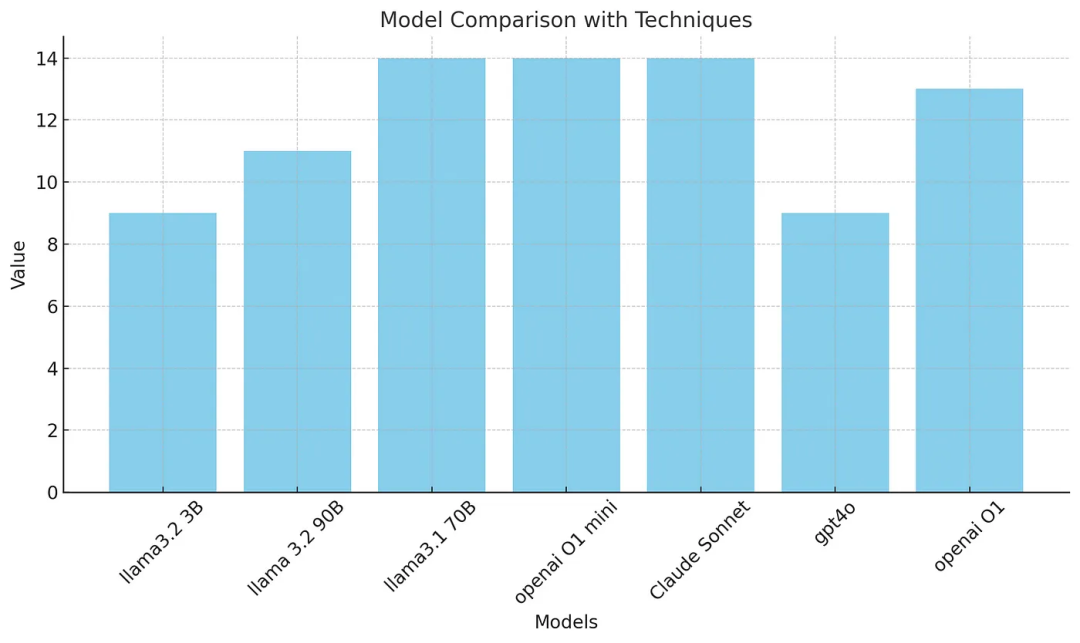
从上述的基准测试可以看到,采用我们的提示词范式后,Claude Sonnet 3.5 在需要较强推理能力的问题上表现优于 O1 和 O1 mini 以及其他小模型。
因此,我建议使用这种提示词范式作为系统提示词来获得更好的表现。
坦白讲,我目前没有足够的计算资源或预算来运行标准基准测试,如 MMLU、MMLU Pro、GPQA 等,如果有人想运行这些测试,请自便。同时,我已将本实验中使用的脚本、数据集以及一些证明过程开源。
代码仓库:
从这次实验中观察到的有关 LLM 的能力和现象:

结 论
我认为大语言模型就像是一个阅读过数百万本书籍的人类,只是它还不知道如何利用这些数据来解决问题。因此,作为 LLM 的研究者和使用者,我们需要教会 LLM 如何利用这些知识来解决问题。
这种推理能力可以被应用于构建高效的工作流自动化,以应对 IT、网络安全、汽车等多个领域的问题。
企业可以部署较小的开源模型作为大模型(例如 gpt4o)的替代方案,用于处理需要推理能力的任务。
我知道,这个实验中的一些结果可能显得过于理想,有点令人难以置信。如果有人想再次进行验证,欢迎使用 GitHub 上的脚本和数据集。
原文链接: