苹果发布新 AI 系统 GAUDI,能在室内生成 3D 场景
近日,苹果 AI 团队发布最新 AI 系统 GAUDI,GAUDI 基于用于生成沉浸式 3D 场景的神经架构 NeRFs,可以根据输入的文字提示生成 3D 室内场景。
GitHub 地址:在此之前,OpenAI 的 DALL-E 2 以及谷歌的 Imagen 和 Parti 等 AI 系统都展示了将文字生成图片的能力,但生成的内容仅限于 2D 图像和图形。
2021 年年末,谷歌通过 Dream Fields 首次展示了新的 AI 系统,该系统将 NeRF 生成 3D 视图的能力与 OpenAI 的 CLIP 评估图像内容的能力相结合。而苹果 AI 团队发布的 GAUDI 则更进一步,能够生成沉浸式 3D 场景的神经架构,并可以根据文字提示创建 3D 场景。
例如,输入“穿过走廊”或“上楼梯”,就可以看到执行这一动作的 3D 场景视频。
据了解,NeRFs 是一种主要用于 3D 模型和 3D 场景的神经存储介质,并能够从不同的相机视角进行渲染。
此前,将生成 AI 扩展到完全不受约束的 3D 场景是一个尚未解决的问题。这背后的原因之一是受限于摄像机位置:虽然对于单个对象,每个摄像机位置都可以映射到一个圆顶,但在 3D 场景中,这些摄像机位置会受到对象和墙壁等障碍物的限制。
对于这个难题,GAUDI 模型的解决方案是:相机姿态解码器对可能的相机位置进行预测,并确保输出是 3D 场景架构的有效位置。
虽然当前 GAUDI 生成的 3D 场景视频质量很低,但这也预示了 AI 在未来新的可能,或许在 AI 的下一阶段,我们可以看到更多惊喜。
GAUDI 背后的技术实现
根据苹果方面的介绍,GAUDI 的目标是给定 3D 场景轨迹的经验分布时,学习得出生成模型。
论文地址:具体技术实现方面,令 X = {xi∈{0,…,n}}表示所定义的经验分布示例集合,其中每个示例 xi 代表一条轨迹。每条轨迹 xi 被定义为相应的 RGB、深度图像与 6DOF 相机位姿的可变长度序列。
苹果 AI 团队将学习生成模型这个任务拆分成两个阶段。首先,为每个示例 x ∈ X 获取一个潜在表示 z = [zscene, zpose],用于表达场景辐射场和在单独的解纠缠向量中的位姿。接下来,给定一组潜在的 Z = {zi∈{0,...,n}},目的就是学习分布 p(Z)。
1.优化辐射场与相机姿势的潜在表示
为每个示例 x ∈ X(即经验分布中的每条轨迹)寻找潜在表示 z ∈ Z。为了获得这一潜在表示,团队采用了无编码器视图,并将 z 解释为通过优化问题[2,35]找到的自由参数。为了将潜在 z 映射至轨迹 x,我们设计了一套网络架构(即解码器),可用于解析相机姿势与辐射场参数。这里的解码器架构由 3 个网络构成(如下图所示):
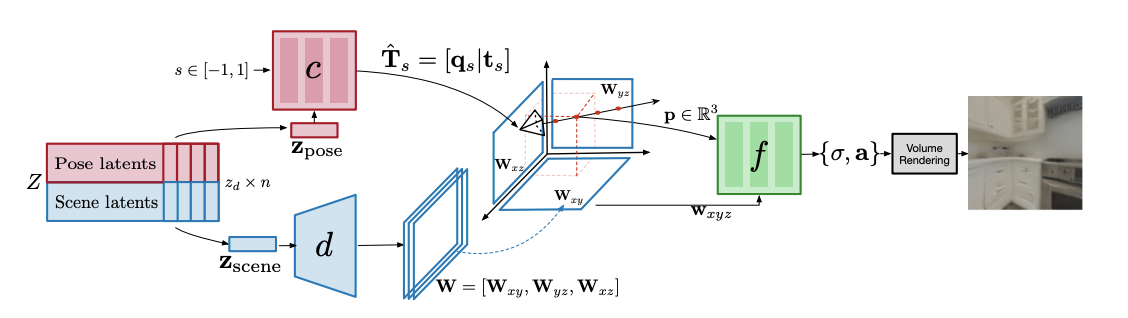
团队还确立了去噪重建目标,用以联合优化θd, θc, θf 和{z}i={0,...,n},详见方程 2。
请注意,虽然潜在 z 是针对每个示例 x 独立优化的,但网络θd, θc, θf 的参数由所有示例 x ∈ X 均摊。与之前的自动解码方法[2,35]不同,每个潜在 z 在训练过程中都会受到与所有潜在模型的经验标准差成正比的加性噪声干扰,即 z = z+βN (0,std(Z)),从而导致收缩表示[46]。在这种情况下,β控制分布 z ∈ Z 的熵与重建项间的权衡:当β= 0 时,z 的分布为指示函数的集合;而β > 0 时,潜在空间则为非平凡结构(non-trivial structure)。使用一个较小的β > 0 值强制获得一个潜在空间,插值样本(或包含与经验分布具有小偏差的样本,即可能从采样后续生成模型中获得的样本)将受解码器支持以被包含其中。
使用两种不同的损失函数对参数θd, θf , θc 和潜在变量 z ∈ Z 进行优化。第一个损失函数 Lscene 负责测量在 zscene 中编码的辐射场与轨迹 xim s 中的图像之间的重建(其中 s 表示帧在轨迹中所处的归一化时间位置),这时需要给定实际相机位姿 Ts。
对 RGB 使用 l2 损失函数,对 4 depth 1 使用 l1 损失函数。第二个损失函数 Lpose 则测量在 zpose 中编码的位姿 T^ s 与真实位姿之间的相机位姿重建差。对平移使用 l2 损失,对相机位姿的归一化四元数部分采用 l1 损失。尽管在理论上,归一化四元数并不一定唯一(例如 q 和-q),但在训练期间并未发现任何经验问题。
2.预先学习
给定一组潜在的 z ∈ Z,这些 z 由对方程 2 中目标的最小化产生。目的是通过学习获得一个生成模型 p(Z),并捕捉其分布(即在最小化方程 2 的目标之后,将 z ∈ Z 解释为潜在空间中经验分布的形式)。为了对 p(Z)进行建模,团队采用了去噪扩散概率模型(DDPM)[15],这是一种新近出现、基于分数匹配[16]的模型。该模型能够通过大量但有限的时间步数,学习马尔可夫链的逆向扩散。
DDPMs 表明,这一逆向过程等效于学习一系列具有绑定权重的去噪自动解码器。DDPM 中的监督去噪目标使得学习这(Z)变得简单且可扩展。由此,我们就能学习得到一个强大的生成模型,该模型能够以无条件/有条件方式生成 3D 场景。为了训练先前的 pθp (Z),采用方程 3 中定义的目标函数。在方程 3 中,t 代表时间步长,~ N (0, I)为噪声,α¯t 为具有固定调度的噪声幅度参数,θp 则表示去噪模型。
在推理期间,团队会遵循 DDPM 中的推理过程以对 z ~pθp (Z)进行采样。首先对 zT~ N (0, I)采样,之后迭代应用θp 对 zT 进行梯度去噪,从而逆向扩散马尔可夫链以获得 z0。接下来,将 z0 作为输入提供给解码器架构,借此重建辐射场和相机路径。如果目标是学习潜在变量 p(Z|Y )的条件分布,则应给定配对数据{z ∈ Z, y ∈ Y },为去噪模型θ增加一个条件变量 y,由此得到θp (z, t, y)。





