前言
回顾一下通俗易懂的红黑树图解(上)，上篇首先介绍了二叉树的定义以及二叉树的查找，然后介绍了红黑树的五点性质以及红黑树的变色、左旋以及右旋等操作，最后结合变色、左旋及右旋详细讲解了插入节点的五种场景。而本篇通俗易懂的红黑树图解(下)是在上篇的基础上讲解红黑树最后一种操作-删除节点，删除节点相对插入节点会复杂一点，但通过分类归纳出不同的场景，能更容易理解和记忆。
○ 红黑树删除
红黑树删除操作包括两部分，一是查找到删除节点，二是删除节点以及删除之后的自平衡。查找节点与二叉树的查找方式一样。而删除操作，当删除节点不存在时，结束本次删除操作；当删除节点存在时，删除节点，然后找到一个节点替换已删除的节点位置，重新连接上已删除节点的父节点与孩子节点。
关键字：
查找节点
替换节点
○ 查找节点
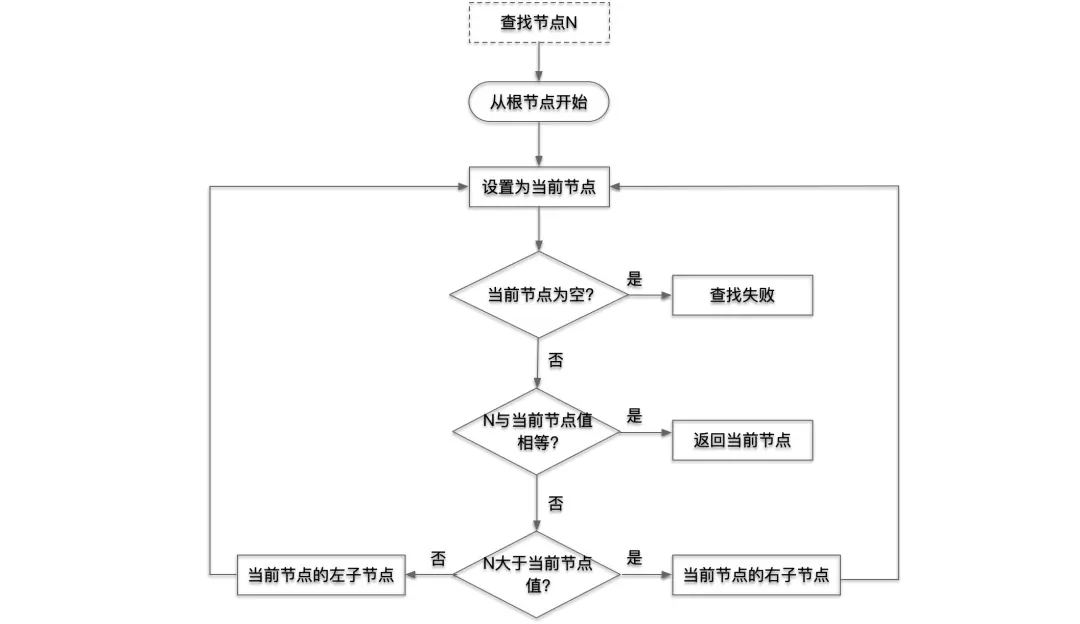
查找删除节点与 二叉树查找节点 (逻辑相同，通过与当前节点值比较，返回当前节点或者继续从左子树或者右子树继续查找。
图片
○ 替换节点
回顾一下二叉查找树的性质：
根据二叉查找树的性质，删除节点之后，可以找到两个替换节点，即可以用左子树中的最大值以及右子树中的最小值来替换删除节点。
删除节点找替换节点又分三种情景：
综上所述，寻找一个节点替换已删除节点位置，在不考虑节点值情况下，可等同于 删除替换节点 。
○ 节点删除
删除节点可等同于删除替换节点，所以节点删除就转换到了替换节点的各种场景。节点删除又分 9 种场景，在如下的描述场景中，场景 2 中的四种情况与场景 3 中的四种情况分别互为镜像，可参照对比着看。
删除场景 1： 替换节点是红色节点
即替换的节点是红色节点，删除之后不影响红黑树的平衡，只需要把替换节点的颜色设成被删除节点的颜色即可重新平衡。
image-20200229234617585.png
删除场景 2 ：替换节点是黑色节点、且是其父节点的左子节点
替换节点是黑色节点时，删除之后破坏了红黑树的平衡，需要考虑自平衡处理。而此又细分为 4 种场景。
image-20200229211126273.png
image-20200229214756335.png
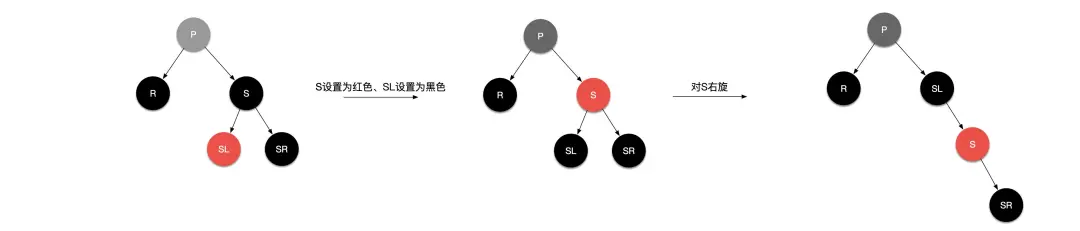image-20200229220440371.png
image-20200229222019042.png
场景 3： 替换节点是黑色节点、且是其父节点的右子节点。（与场景 2 镜像）
image-20200229223345697.png
image-20200229233258336.png
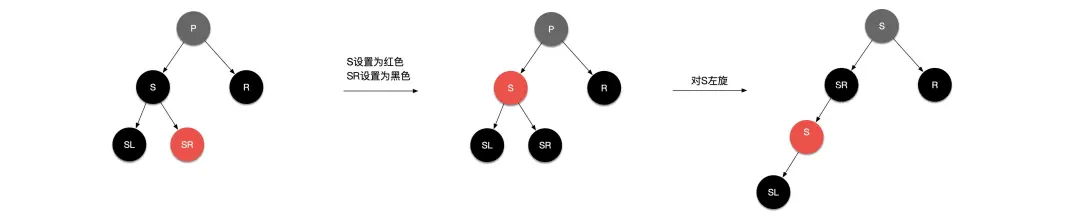image-20200301212153602.png
image-20200229234250179.png
节点删除及平衡代码：
*查找节点*@paramkey节点key值search(key){letnode=this.rootwhile(node){if(key<node.key){node=node.left}elseif(key>node.key){node=node.right}elseif(key===node.key){returnnode*替换u节点，重置v节点*@paramu待删除节点*@paramv子节点constreplace=function(u,v){if(!u.parent){//u是根节点，设置v为根节点this.root=v}elseif(u===u.parent.left){//重置u的父节点的左节点u.parent.left=v//重置u的父节点的右节点u.parent.right=v//重置v的父节点v.parent=u.parent*查找node节点的后继节点findSuccessor(node){while(node.left){node=node.left;returnnode;*删除节点*@paramkey删除节点key值delete(key){constnode=search(key)if(!node){letcolor=node.colorif(!node.left){//左节点为空值fix=node.rightthis.replace(node,node.right)}elseif(!node.right){//右节点为空值fix=node.leftthis.replace(node,node.left)//左右节点都不为空值constsuccessor=this.findSuccessor(node.right)//替换节点的颜色color=successor.color//后继节点只存在右节点或者两个nil子节点情况fix=successor.right//如果后继节点是父节点的非直接子节点if(successor.parent!==node){this.replace(successor,successor.right)successor.right=node.rightsuccessor.right.parent=successorthis.replace(node,successor)successor.color=node.colorsuccessor.left=node.leftsuccessor.left.parent=successorif(color===Color.BLACK){this.balanceDeletion(fix)*删除节点平衡修正*@paramnode节点balanceDeletion(node){while(node!==this.root&&node.color===Color.BLACK){//节点是父节点的左子节点if(node===node.parent.left){//兄弟节点letsibling=node.parent.right;if(sibling.color===Color.RED){//场景2.1:兄弟节点是红色//兄弟节点设置为黑色sibling.color=Color.BLACK;//替换节点的父节点设置为红色node.parent.color=Color.RED;//左旋this.rotateLeft(node.parent);sibling=node.parent.right;if(sibling.left.color===Color.BLACK&&sibling.right.color===Color.BLACK){ //场景2.4:兄弟节点两个子节点都是黑色sibling.color=Color.RED;//再次以父节点为新节点作自平衡处理。node=node.parent;}elseif(sibling.left.color===Color.RED){//场景2.3:兄弟节点的左子节点是黑色，转换到场景2.2.sibling.left.color=Color.BLACK;sibling.color=Color.RED;//对兄弟节点右旋this.rotateRight(sibling)sibling=node.parent.right;if(sibling.right.color===Color.RED){//场景2.2：兄弟节点的右节点是红色sibling.color=node.parent.color;node.parent.color=Color.BLACK;sibling.right.color=Color.BLACK;//对父节点左旋this.rotateLeft(node.parent);//左旋之后，红黑树重新平衡node=this.root;//节点是父节点的左节点letsibling=node.parent.left;if(sibling.color===Color.RED){//场景 3.1：替换节点的兄弟节点是红色sibling.color=Color.BLACK;node.parent.color=Color.RED;this.rotateRight(node.parent);sibling=node.parent.left;if(sibling.right.color===Color.BLACK&&sibling.left.color===Color.BLACK){//场景3.4：替换节点的两个子节点都是黑色sibling.color=Color.RED;//再次以父节点为新节点作自平衡处理。node=node.parent;}elseif(sibling.right.color===Color.RED){//场景3.3:兄弟节点的右子节点是红色sibling.right.color=Color.BLACK;sibling.color=Color.RED;this.rotateLeft(sibling);sibling=node.parent.left;if(sibling.left.color===Color.RED){//场景3.2：兄弟节点的左子节点是红色sibling.color=node.parent.color; node.parent.color=Color.BLACK;sibling.left.color=Color.BLACK;this.rotateRight(node.parent);node=this.root;node.color=Color.BLACK;红黑树应用
红黑树广泛用在 Java 的集合框架 (HashMap、TreeMap、TreeSet)、Nginx 的 Timer 管理、Linux 虚拟内存管理以及 C++ 的 STL 等等场景。
在 Linux 内核中，每个用户进程都可以访问 4GB 的线性虚拟空间，虚拟空间往往需要多个虚拟内存区域描述，对这些内存区域，Linux 内核采用了链表以及红黑树形式组织。内存区域按地址排序，链接成一个链表以及一颗红黑树，寻找空闲区域时只需要遍历这个链表，在发生缺页中断时通过红黑树快速检索特定内存区域。
总结
红黑树的删除操作就基本介绍完了，总结一下删除操作就是，删除节点等同于删除替换节点，若替换节点是红色节点时，直接删除不会影响平衡；若替换节点是黑色节点时，就需要借用兄弟节点的右子节点、左子节点或者兄弟节点。
红黑树最吸引人的是它的所有操作在最差情况下可以保证 O(logN) 的时间复杂度，稳定且高效。例如要在 10 万条 (2^20) 数据中查找一条数据，只需要 20 次的操作就能完成。但这些保证有一个前置条件，就是数据量不大，且数据可以完全放到内存中。在数据量比较大时，因为红黑树的深度比较大造成磁盘 IO 的频繁读写，会导致它的效率低下。
另外推荐Data Structure Visualizations网站，它包含非常多的数据结构方面的可视化算法题。其中就有红黑树的算法，对照着在线生成的红黑树看，会更容易理解红黑树中各种操作场景。
头图：Unsplash
作者：泰阿
原文：原文：通俗易懂的红黑树图解(下)
