导读 :自动驾驶技术研发对于“安全第一”的追求是毋庸置疑的,但是这中间可能就忽视了舒适性。
因此,今天我想给大家分享的是,自动驾驶研发如何在兼顾安全性的同时,保证乘客体验的舒适。往细一点说,就是如何通过优化算法在规划和控制模块中找到安全性和舒适性的平衡点。
01 安全性和舒适性的定义

安全性的定义其实比较好理解,一般包括不发生碰撞和遵守交通规则(交通灯、停车标志、限速)。
而舒适性则受下面两个指标影响:
在二者的定义基础上, “安全舒适两不误”也就意味着在遵守交规且不发生碰撞的基础上,控制好行驶时的加加速度和行进路线的曲率变化率 。
02 规划和控制的定义
规划(Planning)和控制(Control)是自动驾驶最底层的部分, 决定了车在路上如何行使 。
一般来说,规划所需要的输入(Input)信息包括:地图信息,起点终点,障碍物预判,交通标志以及感知信息,即周围的物体位置、大小、速度、方向等。
借助这些输入信息,规划模块可以输出(Output)一段时间的行驶轨迹(Trajectory),即某一个时间无人车行驶到到某个位置的函数(Xt~Yt)。
而规划输出的轨迹正好是控制(Control)模块的两项输入之一,另一项输入是车辆自身的状态,包括车的位置、heading(行驶朝向)、速度、加速度、角速度等信息。
而控制模块会输出以下两类信息:
简单来说,控制的目的是让自动驾驶车能够精准实现规划模块给出的行驶指令。

上面就是规划和控制的简单定义。当然,这里我也留下一个思考(上图标灰的地方):对于规划模块而言,是否必须知道车辆的实时位置信息?
答案是,有无都是可以。规划和控制模块都能有相对应的做法和方案。
03 规划上,如何实现安全性和舒适性?
安全性
前面已经说到,规划(Planning)为的是输出一个 trajectory(时间到位置的函数):X(t)=(x(t),y(t))T,而这个行驶路径需要同时保证安全性和舒适性。
实际上,规划(Planning)是一个优化问题。对于一个优化问题来说,我们需要通过设计 constraints (约束条件) 来保证行驶安全。
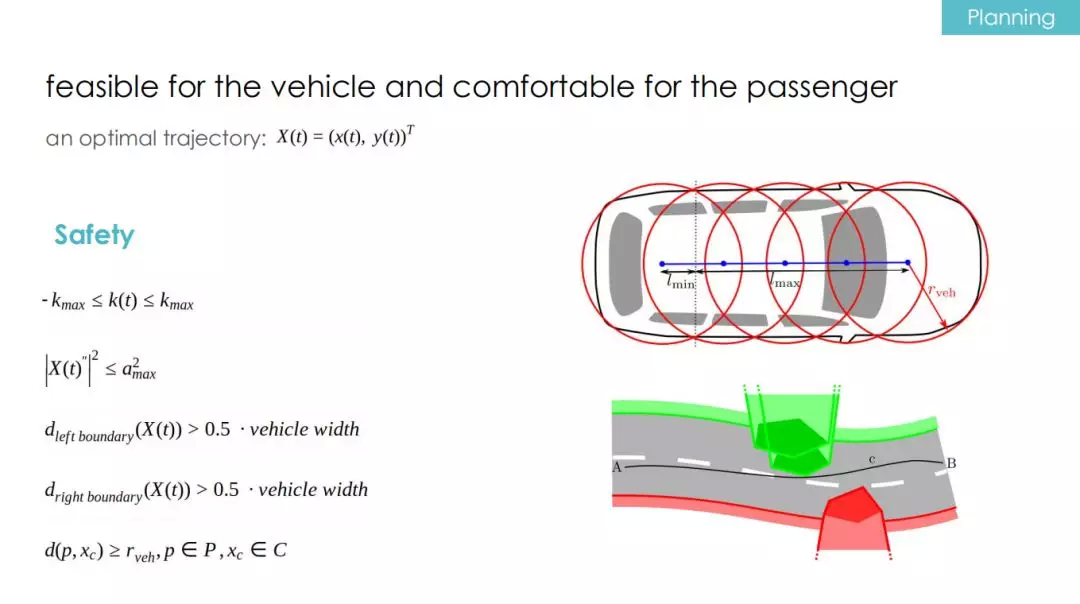
上图里列举了一些最基本的约束条件。
首先,规划模块不能忽略车的物理特性,比如方向盘的最大角度,对应的就是曲率的最大值、最小值等。
其次,明确车辆刹车和油门的极限,这对应的就是加速度的极限。
第三,当自动驾驶车在道路上行驶时,为了不出现压线的情况,车到左右 boundary(车道线)的距离也需要纳入规划中。
第四,自动驾驶肯定不希望车辆发生任何碰撞。我们可以通过取车轴上一系列等半径的圆来覆盖车身,并采用若干个凸的多边形表示车身周围的物体,那么,当车轴上所有的圆心到凸多边形的距离大于半径时,自动驾驶车就不会与凸多边形(障碍物)发生碰撞。
舒适性
介绍完安全性,下面介绍规划模块是如何实现驾驶的舒适性。前面提到过,舒适性越高,意味着加速度变化率越小,以及曲率的变化率越小。那么对应的 cost function(代价函数)就比较好设定了,即加速度+加速度变化率+曲率+曲率的变化率。

虽然整个模型设计起来比较简单,但是 constraints(约束条件)和 cost function(代价函数)的求解却比较复杂(如上图),尤其是系统实时求解 k(t)和 k(t)’的耗时会比较长,解起来也比较难。这时候我们可以换个思路,把问题转换下。
前面也提过,规划问题其实是为了解出一个时间到位置的函数,而 L4 级自动驾驶车一般会行驶在结构化的道路上,这也意味着规划模块具备地图的信息,那么问题就可以进行转化——把(x,y)坐标系转化为下图的(l,s)坐标系。

s 沿着道路中线(reference line)的方向,l 则是垂直于道路中线的方向。于是,问题就转化成了求解 s(t)和 l(s)的问题,我们希望得出,自动驾驶车在 t 时刻应该走到 s 上的哪个位置;以及走在这个位置时,该车距离 s 的左右偏离是多大。
最终,一个复杂问题就转化成三个子优化问题: 一个横向优化、纵向优化以及中线问题(s 方向是车辆的纵向规划,l 方向为横向规划) 。
接下来我想仔细说一说这三个子问题。
子问题一:横向优化

上图中右侧展示了一条路,中间的线是 reference line(参考线),其中“0”点就是车当前所在的位置,“-1”,“-2”是车之前的坐标位置,接下来的“1,2,3,4”……就是规划模块的输出结果,也就是车未来的位置。
这条路的左右两边是 boundary(道路边界/车道线),图中的半圆对应着路面上的障碍物。横向规划求解的是正是每一点的 l 坐标,也就是到中心线的偏离量。
对于横向优化问题,我们同样可以从安全性和舒适性两方面考虑。
安全性方面,取决于横向优化问题的 constraints(约束条件),一般要求 l 不能太小,也不能太大,即不能压左边线,也不能压右边线,同时不能碰到左右两边的障碍物。
舒适性方面,我们则设计成 cost function(代价函数),一般要求路线的曲率越小越好,曲率变化率越小越好。如果我们的参考线是一条完美的参考线,那么曲率就可以用一个相对曲率来表示。
对于一个优化问题来说,cost function(代价函数)变成了标准的二次函数,同时,所有的 constraints(约束条件)都是一次的。
那么,这就成了一个标准的 QP(Quadratic programming,二次规划)问题,不仅如此,这还是一个 box constraint(闭箱约束)的 QP 问题,我们就能够非常快速求出优化的结果。
子问题二:纵向优化
纵向优化求解的则是 t 到 s 的函数。
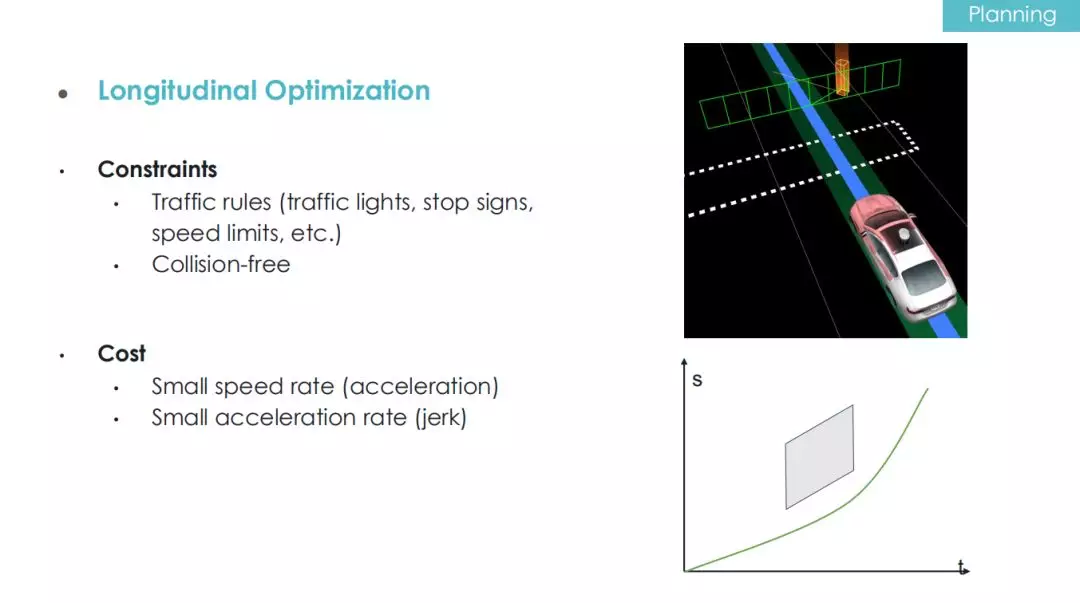
对于纵向规划的来说,安全性要求我们保证车辆不能发生前后方向上的碰撞。以上图右侧为例,此时有个行人正在过马路,规划模块会将行人的行为可以转换成(t,s)坐标,展示在坐标图里(上图)是一个平行四边形。
此时,面对这个行人,如果自动驾驶车选择让路,纵向规划解出来的曲线就应该在平行四边形的下方;如果选择超过这个行人,那么这条曲线应该从上面绕过去。
在纵向规划上,舒适性体现在加速度越小越好,以及加速度的导数越小越好。可见,纵向和横向规划涉及的 constraints(约束条件)和 cost function(代价函数)都非常相似。
子问题三:中线生成
同样,中线的生成也是一个优化问题,自然也会涉及到 constraints(约束条件)和 cost function(代价函数)。

中线设定的约束条件首先是不能压边界(车道线),同时要符合曲率的限制。对于 cost function(代价函数)来说,希望达到的目标是中线的曲率越小越好,曲率的变化率越小越好。这样来看,中线问题也是求解 k(t)和 k(t)’的函数问题。
问题似乎又绕回去了,为了舒适性,我们还是需要求解非常复杂的方程吗?
并不是。由于中线是可以离线生成的,所以不需要在线计算,这些问题能放在服务器中进行并行的计算。
这里,我想增加一个值得思考的问题。前面提到,生成中线的前提是具备道路的信息,即道路左右的 boundary(车道线边界)。然而当自动驾驶车处在一个路口内,路面并没有车道线,这种环境下应该如何处理参考线呢?欢迎大家留言探讨。
04 控制上,如何实现安全性和舒适性
毕竟自动驾驶控制的是一辆车,而不是一个点,所以在详细介绍自动驾驶控制模块之前,我想先介绍一个模型。
Bicycle model (自行车模型)
控制的模型有很多,而且非常复杂,需要考虑车辆的很多因素,包括引擎,变速箱,轮胎,悬架等等。为了讲好这个问题,我先给大家介绍一个最简单的模型 Bicycle model(自行车模型)。
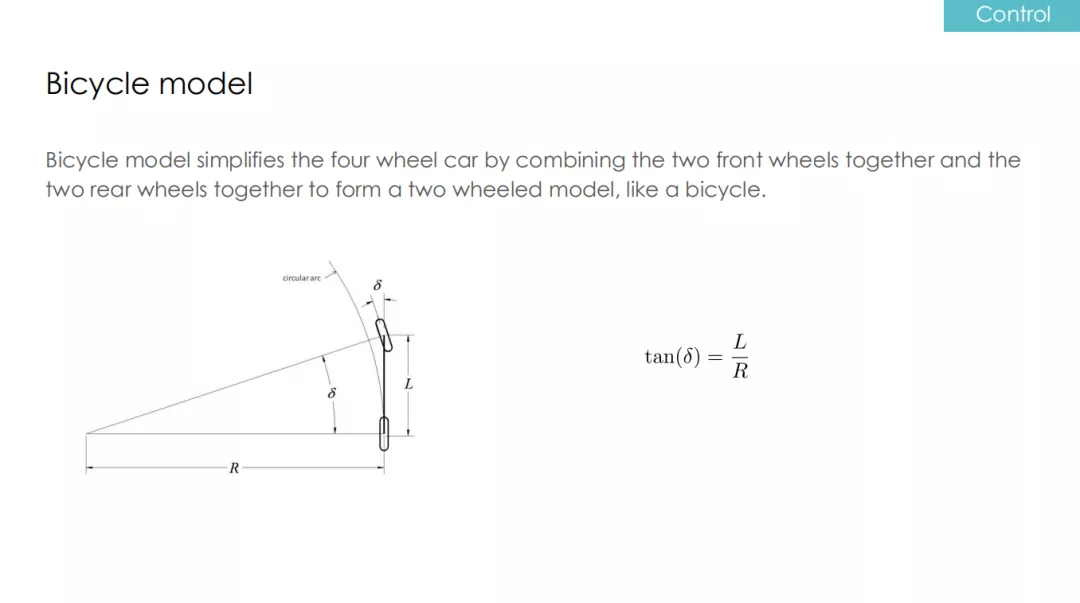
首先,假设自动驾驶车辆的车宽为 0,可以想象成是两个前轮靠在一起,两个后轮靠在一起(上图)。
这个假设就意味着前轮的转角和转速都是一致的,当然现实中车辆的四个轮子的转角和转速都是不一样的,所以这个模型只是在做一个最简单的假设。基于这个假设,当得知前轮转角转了δ时,我们也可以通过几何关系算出后轴的转弯半径是多大。
前面把车假设成了“自行车”,下图展示了它的行驶轨迹,那么,哪一条是前轮的,哪一条是后轮的?车是往左边行驶还是右边行驶?

首先,基于自行车模型的假设,后轮的侧向速度为 0,所以后轮永远都是朝向前轮行驶的,在红线上画一条切线,会发现它没有穿过蓝线,所以它不是后轮。在蓝线画一条切线,它穿越了红线,因此蓝线是后轮的轨迹。
车往那边走呢?我们继续在蓝线上画一条切线,这条切线和这条红线还是有两个交点。实际上,交点和切点的距离就是车的轴距,并且由于轴距是固定的,所以这辆行驶的车就如图中黑线所示。这个问题的答案是:红线代表前轮,蓝线代表后轮,以及它是向右行驶的。
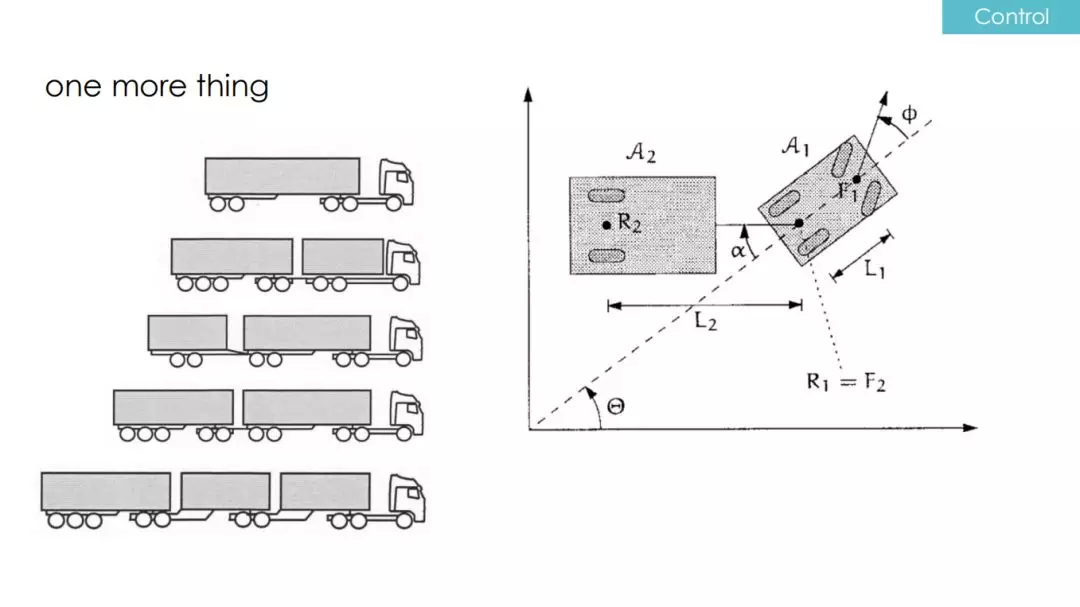
总结来说,对于只有两个轴并且通过前轮转向的车辆,一般可以转换成 Bicycle model(自行车模型)。但在真实路上行驶的往往不只是小汽车,比如还有货车,而货车可以分为两个部分,车头与后挂。
对于货车的控制,如果还是采用自行车模型进行假设(上图),则 A1 是车头,A2 是挂车,F1 为车头的前轴,R2 认为是挂车的后轴。在这个模型中,我们认为挂车的前轴和车头的后轴是同一个点 R1=F2,车头的轴距是 L1,挂车的轴距是 L2,当得知车头的前轴转了ϕ角度时,控制模块可以得到车头后轴的转弯半径。
那么,挂车的后轴轨迹会呈现出一条什么样的曲线?这个问题也欢迎大家留言讨论,毕竟现实生活中,路面上不止有一种车,自动驾驶从业者可以多思考下,各类车型的运动行为应该是什么样的。
横向控制(Lateral Control)

上图中紫色曲线是 Planning(规划模块)输出的目标轨迹,图中的蓝点是自动驾驶车此刻的位置,蓝色的箭头是车现在的行驶方向。
可以看到,自动驾驶车辆与规划轨迹存在一个侧向的偏差,因此横向控制的目标就是使车辆实际轨迹和目标轨迹的侧向偏差越小越好,同时车在某个时刻的 heading(朝向)与规划轨迹曲线对应点朝向的误差越小越好。
预瞄算法就是横向规划中常用的一种:首先会选定一个预瞄点,横向控制的目标就是到预瞄点时,侧向误差和 heading(朝向)的与目标轨迹的误差越小越好。这里的控制变量就是刚才说的曲率,所以横向控制又转化为了一个优化问题。
纵向控制(Longitudinal Control)
同样的,在纵向控制上,我们也可以选一个预瞄点,希望达到的目标是自动驾驶车速(v)与规划轨迹的误差越小越好,位移(s)与规划轨迹的误差越小越好,于是纵向控制也可转为优化问题。
总结来看,不管是对于 Planning(规划)还是 Control(控制),最终都可以转化为优化问题。
自动驾驶规划模块对舒适性和安全性的探索,重点就在于设计优化问题中的 constraints(约束条件)和 cost function(代价函数)。
而控制模块则在于预瞄点的选择,控制模块最终的目标就是自动驾驶车更精准地跟随规划轨迹,当预瞄距离越近,控制就越精准,当预瞄距离越远,控制量更加 smooth(平滑),体感可能更加舒适,但误差可能越大。
最终,我们都能坐上既安全又舒适的自动驾驶车。今天的分享就到这里,谢谢大家。
作者介绍 :
孙浩文
Pony.ai | Tech Lead
本文来自>
原文链接 :