
1.背景
当我们打开导航,开车驶向目的地的过程中,有时候会碰到这样的问题:前方明明没有路,可能在施工封闭,可是导航仍然让我们往前开车,以至于我们无法顺利到达目的地。全国道路千千万,每天都有巨量的道路变得不可通行,那么如何动态的识别出哪些道路走不通了呢?

图中所示即为因封路事件导致的导航路线改变
道路不通往往导致该条道路汽车流量突然降低。监控汽车流量的变化是挖掘封路事件的重要指标。但是,目前业务中遇到的一个重要问题是,针对汽车无法通行的封路事件,行人、自行车可能都可以穿行,这些行人、自行车等的噪声流量大大削弱了道路流量变化。
因此,如果能够对行人、自行车、汽车的轨迹进行分类,就可以对道路流量的噪声进行过滤,仅仅关注汽车流量,流量随着封路事件的变化将更为显著,从而便于道路封闭的挖掘。本文主要针对非机动车、机动车分类探索轨迹分类问题。
2.样本获取与标签制定
由于轨迹数据缺少原始真值,我们将用户导航模式作为轨迹分类的伪标签。例如当时用户采用汽车导航,其轨迹对应的标签即为汽车。由于汽车导航数据远远多于非机动车,不同伪标签样本比例差异巨大,存在严重的样本不平衡问题。此外,用户导航模式与用户实际出行方式可能并不一致。比如有些用户可以根据汽车导航步行到达目的地。下文介绍的标签- 概率混合贝叶斯模型 将分析并试图解决上述 2 个问题。
3.特征分析
可以将轨迹分类相关特征划分为 5 类。分别是:
下面以轨迹开始时间特征为例,解释该特征的物理意义。其概率密度函数如下所示(drv,汽车;byc,自行车;wlk,步行):
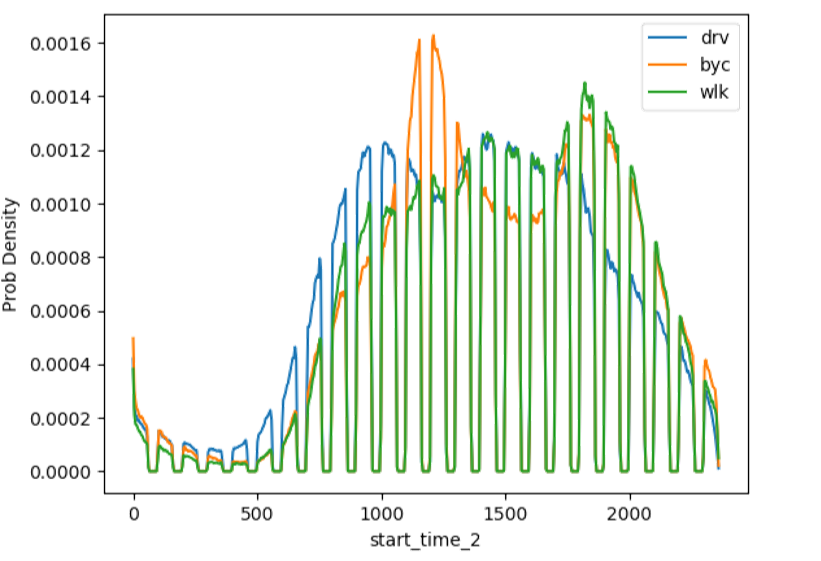
早晨(5:00~10:00)汽车轨迹概率较高,可能是早高峰导致。
午时(11:00~13:00)自行车轨迹概率较高,可能是由于外卖送餐。
傍晚(17:00~20:00)步行、自行车概率均较高,可能是由于下班散步以及外卖送餐。
4.贝叶斯模型的概率分布视角
选择基于贝叶斯分类器进行改进的原因如下:

4.1 标签-概率混合贝叶斯模型
当前轨迹分类问题为样本不平衡(Data Unbalanced)标签不准确(Noisy Label)问题。

Tanaka 等人基于卷积神经网络提出了伪标签损失函数,通过交叉熵损失函数与伪标签损失函数的迭代优化完成了错误标签的修正[2]。受此启发,贝叶斯模型同样能够建立伪标签损失函数完成样本清洗。
我们基于贝叶斯分类器的分类结果,提出基于伪标签极大似然估计的伪标签损失函数,完成错误样本清洗,再迭代完成贝叶斯分类。该模型的迭代流程如下图所示。
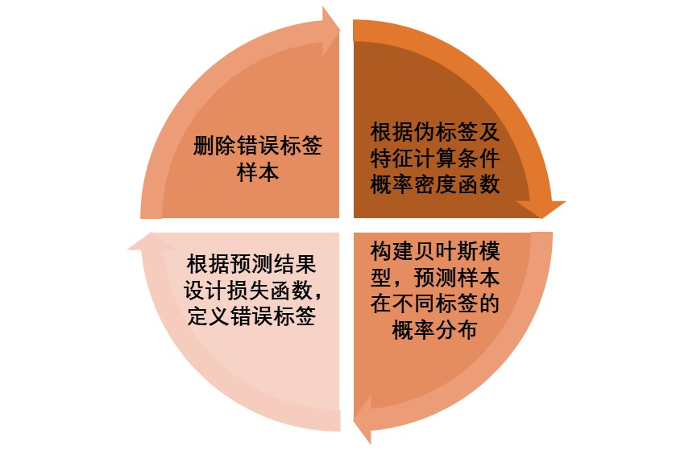
标签-概率混合优化贝叶斯模型迭代流程。


4.2 联合概率密度函数计算
由于贝叶斯分类器假设各变量相互独立,因此不可避免的会对一些场景下的样本产生错误预测。例如,外卖骑手以及快递员应当被判定为非机动车。这种类型轨迹长度可能较长(超过 10 公里),最大速度适中(小于 50 公里每小时)。在假设行驶距离与最大速两个特征相互独立的情况下,容易错误地把外卖骑手以及快递员的行驶轨迹判定为汽车。
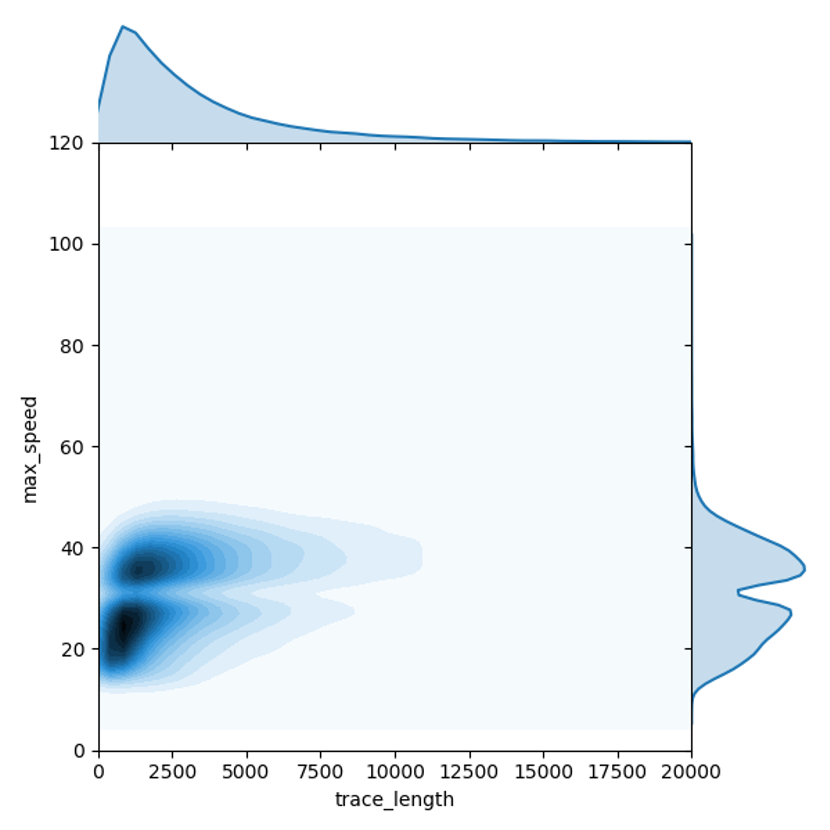
自行车轨迹行驶距离以及最大速度联合概率密度函数
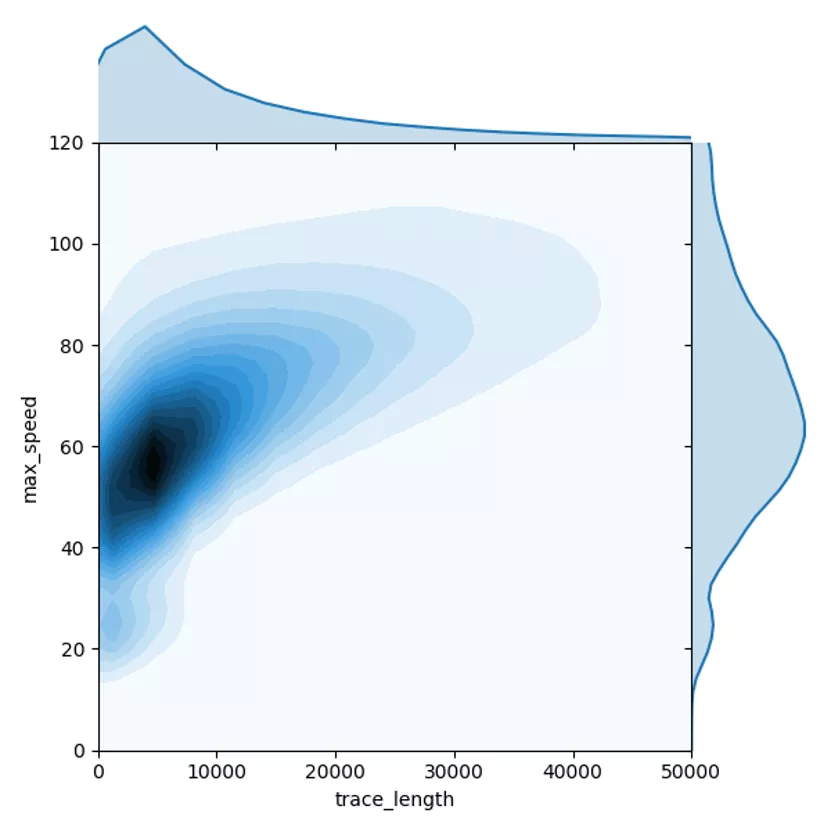
汽车轨迹行驶距离以及最大速度联合概率密度函数
但是,行驶距离与最大速两个维度的特征并不相互独立。上图构建了针对汽车轨迹这两个维度的联合概率密度函数,可以发现,对汽车轨迹而言,行驶距离越长,最大速可能越高,当汽车行驶距离超过 10 公里时,其最大速度小于 50 公里每小时的可能性很低。因此,通过构建行驶距离与最大速度两个维度的联合概率密度函数,替换两个独立概率的相乘,可以帮助解决长距离非机动车轨迹被误判为汽车的问题。
4.3 基于贝叶斯的轨迹分类实验结果
评测团队抽样约 100 条数据并人工标记真值。最终模型分类效果如表所示。
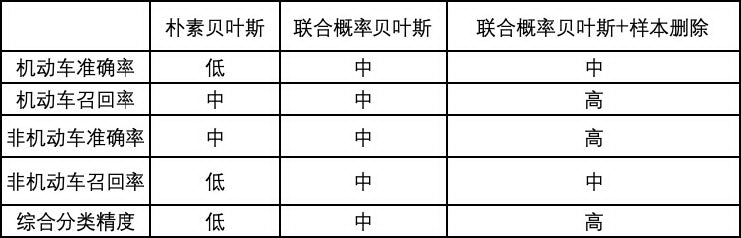
5.深度学习模型的图像编码视角
由于轨迹数据缺少原始真值,我们将用户导航模式作为轨迹分类的伪标签。例如当时用户采用汽车导航,其轨迹对应的标签即为汽车。本次基于深度学习的探索不考虑标签噪声的问题。
5.1 轨迹信息的两种观察方式
深度学习的优势在于能够从原始数据中学习到有效信息,无需人工挖掘特征。针对轨迹数据的特点,存在两种观察轨迹的方式,分别是时间序列与空间分布。
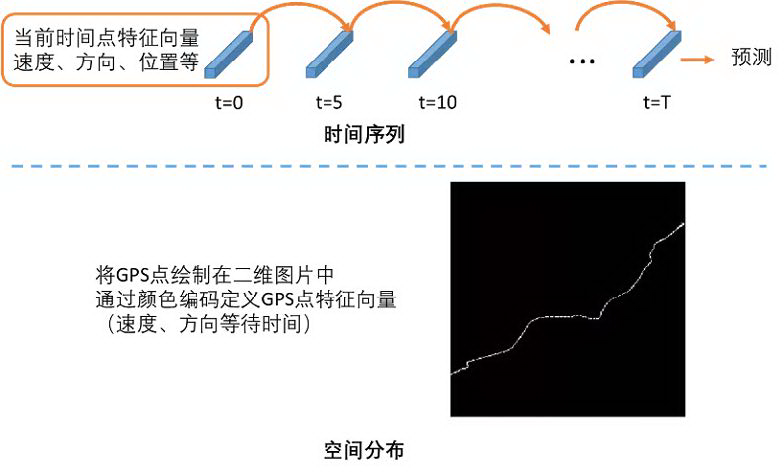
时间序列 :轨迹当中的 GPS 点数据随时间推移依次上传至数据库中。轨迹数据天然具备时间序列属性。因此,可以采用 TCN 或 RNN 构建模型,学习轨迹中的时间序列信息,完成轨迹分类。
空间分布 :将轨迹数据绘制在地图中,则轨迹构成图片中的一条线。如果能够将速度、方向、等待时间编码到线的颜色当中,则能够采用 CNN 从轨迹图像中学习到有效信息[3]。
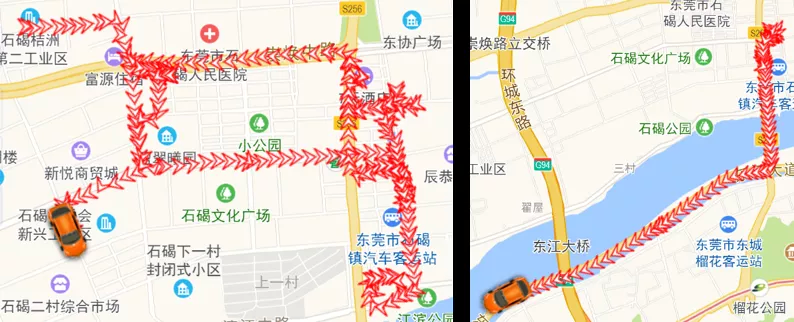
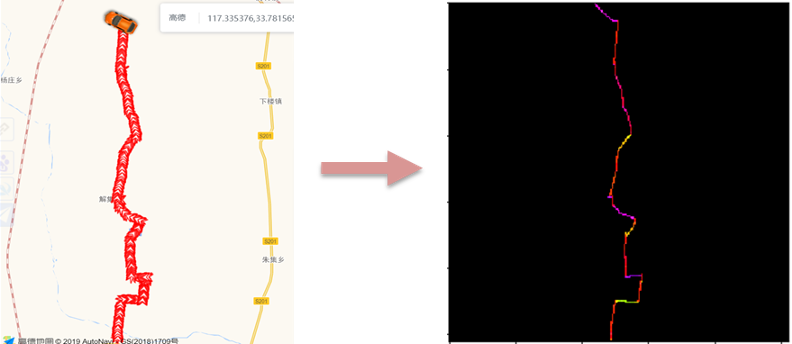
图左侧大概率为快递员轨迹,图右侧大概率为汽车轨迹。GPS 点的空间分布能够为轨迹分类提供有效信息。因此,我们采用空间分布模式构建模型,探索基于深度学习的轨迹分类。
轨迹颜色编码:从 GPS 点中获取的主要信息为速度、方向、等待时长。将这 3 个维度的信息进行轨迹颜色编码有 2 种方式,分别是 RGB 编码与 HSV 编码。其中 HSV 即色相(Hue)、饱和度(Saturation)、亮度(Value)。
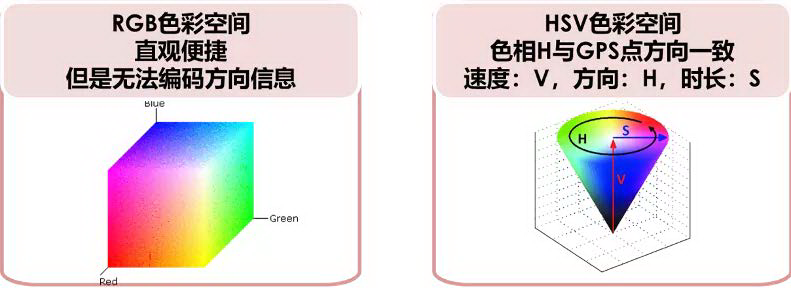
由于方向信息为 0~360 度的角度值,与 HSV 色彩空间种的色相 H 完全一致。因此,本文采用 HSV 色彩空间对速度、方向、等待时长进行编码,编码方式为速度:V,方向:H,时长:S。编码后将轨迹缩放为 256×256 的图片。对地图轨迹的编码结果如下图所示。
5.2 双流神经网络模型
基于编码生成的轨迹图片依然缺失一些重要信息,包括将轨迹缩放至 256×256 图片的缩放因子,以及 GPS 点所在的位置。可以将轨迹匹配结果中通过国道、省道、城市快速路等不同类型道路的比例构造出特征集表征 GPS 点所在的位置信息,加入缩放因子构造一个一维静态特征向量。
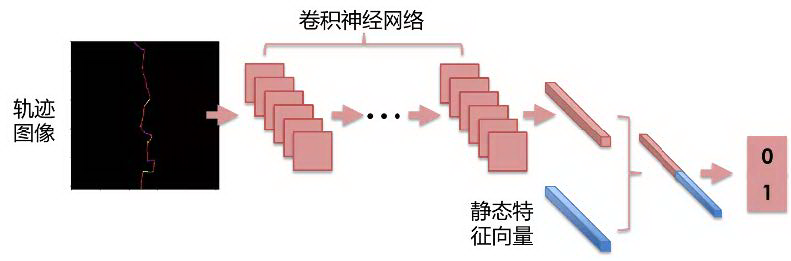
将卷积神经网络学习到的特征向量以及该一维特征向量合并,最终通过全连接层完成轨迹分类。最终卷积神经网络选择 ResNet50 结构。
5.3 基于深度学习的轨迹分类实验结果
评测团队抽样约 100 个样本,人工标记真值。

如上表所示,以人工标记标签为真值验证深度学习模型,深度学习模型能够取得有效的轨迹分类精度,但是最终分类效果弱于提出的贝叶斯模型。可能的原因有如下几点:
6.小结
轨迹分类对于准确及时地挖掘道路封闭事件具有重要意义。本文从给予概率密度分布的贝叶斯模型视角与基于轨迹点图像编码的深度学习视角分别探索了轨迹分类可能的技术方案。未来轨迹分类模型还可以从聚焦应用场景,优化应用以及拓展上游数据,优化特征两个方面进行改进。
参考文献
[1].Frénay B, Verleysen M. Classification in the presence of label noise: a survey[J]. IEEE transactions on neural networks and learning systems, 2013, 25(5): 845-869.
[2].Tanaka D, Ikami D, Yamasaki T, et al. Joint optimization framework for learning with noisy labels[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 5552-5560.
[3].Liu Y, Wang X, You W. Non-intrusive Load Monitoring by Voltage-Current Trajectory Enabled Transfer Learning[J]. IEEE Transactions on Smart Grid, 2018.
原文链接 :
机器学习在高德地图轨迹分类的探索和应用





