在模型开发完成之后,一个必不可少的步骤是对建立的模型进行评估,评估其是否满足使用的需要。模型评估有着一套相对标准的模型评价指标,现在按照不同的模型类型进行描述。
混淆矩阵
关于二分类模型的评价指标,混淆矩阵(Confusion Matrix)可以解释大部分的概念,如下所示:
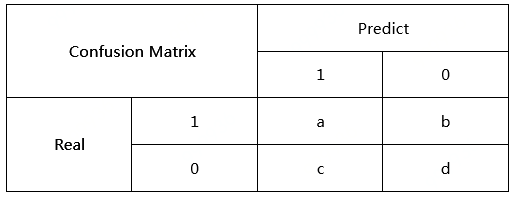
基于混淆矩阵衍生的模型评价指标有:
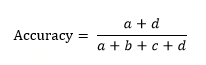
准确率(accuracy)衡量的是分类正确的样本占总样本数量的比例。在一定情况下,准确度可以很好的评价模型的效果,但是,在某些情况下,其评价效果可能会有差异。比如在样本比例相差过大时(原样本为 1 的样本占总样本数 99%),将所有的样本均判定为 1 的分类器将取得 99%的 accuracy,将远远好于其它分类器大量训练所得到的结果。故在此基础上,从不同方面出发,有不同的衡量指标。
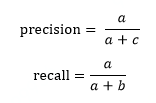
precision 是预测为 1 的样本里面,真实标签为 1 的样本占比。recall 是实际为 1 的样本里,预测为 1 的概率。在通常情况下,precision 高时 recall 偏低,recall 高时 precision 偏低。以挑选西瓜为例,如果以 precision 作为衡量标准,则尽可能的选取有把握好的西瓜,这样 a 和 c 就会相对较小,b 和 d 相对较大,则 Recall 较低。如果以 recall 为衡量标准,则是希望尽可能的将好瓜选出来,错判相对会较多,故 a 和 c 相对较大,b 和 d 相对较小,故 precision 相对会降低。
在不同的使用场景下,对于 precision 和 recall 各有侧重。以信贷领域为例,在进行信用评级时,我们希望 precision 尽可能的大,才能尽可能的避免资金的损失。在进行信贷营销时,我们希望 recall 尽可能的大,才能营销到足够多的目标群体。
对于一般来说,为了平衡 precision 和 recall,可以采用 F score 作为评价标准
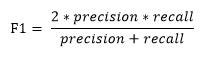
F1 的值同时受 precision 和 recall 的影响,取值范围为 0 到 1 ,越大代表模型效果越好。
ROC 曲线
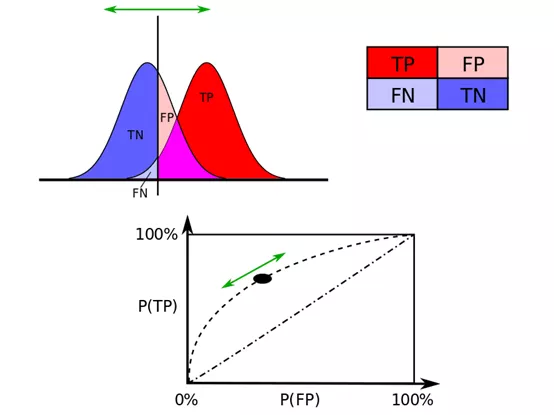
对于二分类模型来说,输出结果标签(0 还是 1)往往取决于输出的概率以及预定的概率阈值,常见的阈值是 0.5,输出概率大于 0.5 的判定为正样本,小于 0.5 的判定为负样本。如果增大阈值,对应的预测为正的样本数会减少,一般而言,precision 会升高而 recall 降低;如果减小阈值,对应的预测为正的样本数会增加,precision 会降低而 recall 升高。实际上,阈值的选取一定程度上影响了分类器的分类能力。我们希望一个好的分类器,在任何阈值情况下,都能有一个比较好的效果。为了衡量这个不区分阈值的分类器优劣,ROC 曲线表现出很好的区分能力。

上面第一个图两个分布分别为负样本和正样本的概率分布,横坐标为最后模型的打分,中间的竖线表示阈值。可以看到,随着阈值的上升,TN 和 FN 增大,TP 和 FP 减小。第二个图画出了 ROC 曲线,ROC 曲线横轴表示 FPR(False Postive Rate),即,代表分类器中预测的正类中实际负实例占所有负实例的比例,纵轴表示 TPR(True Postive Rate),即代表分类器预测的正类中实际正实例占所有正实例的比例。由定义可见,随着阈值的增高,TPR 和 FPR 均下降,对于 FPR,我们希望其越小越好,对于 TPR,我们希望其越大越好。将一个模型不同阈值情况用线串联起来,得到的曲线就是 ROC 曲线,ROC 曲线越靠近左上角,模型效果越好,曲线下面积记为 AUC,AUC 越大,表示模型整体区分效果越好。
模型评价方法多种多样,在不同的使用场景下各有偏重,在实际业务上,需要根据当前业务发展情况,选择合适的评价方法和模型。