近期,前百度研究院副院长李平等人开源了多年的研究成果 Fast ABC-Boost 机器学习包。
据悉,该研究十多年前就已经开始,2010 年,李平发表了题为“Robust LogitBoost and Adaptive Base Class (ABC) LogitBoost”的论文,2018 年的图灵奖得主 Yoshua Bengio 当时还与人讨论了李平在树模型和 boosting 上的工作。
根据介绍,李平在 2007 年斯坦福大学博士毕业后,曾在任康奈尔大学和后罗格斯大学任教,并于 2013 年成为计算机系和统计系两系的终身教授。其主要研究方向是算法学习、高效检索、机器存储、数据流和推荐等,曾获得 NIPS2014 最佳论文奖、ASONAM2014 最佳论文奖、KDD2006 最佳论文奖,以及美国空军和青年科学家奖(AFOSR-YIP)、美国海军杰出数据科学家奖(ONR-YIP)等奖项。
2020 年 1 月,李平开始担任百度研究院副院长,其团队与百度的凤巢广告、Feed 流、搜索、百度知道、中文输入法、百度地图等业务部门展开合作,把研究成果应用到各项产品中。
在 Fast ABC-Boost 开源后,李平表示:“这个工作太实用了,本身影响力是巨大的,只不过有点可惜绝大部分使用者不会知道(也未必关心)原作者是谁。不过回想起来,我自己并没有太去关心已经完成的工作,而是把精力放在做完全不同的新研究。这样反而收获更大。”
根据介绍,Fast ABC-Boost 的精度超过了经典的 XGBoost、LightGBM。本文将对这项研究工作进行详细解读。
概览
“Fast ABC-Boost”软件包是作者在康奈尔大学、罗格斯大学和百度研究院十多年工作的成果。下面是作者在康奈尔大学和罗格斯大学的课堂授课稿件:
••15–77)
一些机器学习研究人员可能仍然记得在 2010 年论坛上的一些讨论。在“Robust logitboost and adaptive base class (abc) logitboost”(2010 年,by Li)论文中,“Robust LogitBoost”和“Adaptive Base Class Boost”被作者提出来了。当时,研究人员很好奇,在深度学习研究人员开发的数据集上,增强树算法(boosted trees) 与深度神经网络相比,为什么还是非常有效。
自那次讨论以来,已经过去了十年。不必多说,深度神经网络在许多研究和实践领域取得了巨大的成功。在作者开发了这些增强树算法之后,比如:“Learning to rank using multiple classification and gradient boosting”论文(作者等人,2007)、“Adaptive base class boost for multi-class classification”论文(作者等人,2008)、“ABC-Boost: Adaptive base class boost for multi-class classification”论文(作者等人,2009)、“ Fast abc-boost for multi-class classification”论文(作者等人,2010a)、“Robust logitboost and adaptive base class (abc) logitboost”论文(作者等人,2010b)。他精力转移到其他许多有趣的研究课题,包括随机素描(randomized sketching)、哈希方法(例如,Li and Zhao ,2022b)、近似近邻搜索和神经网络排序(例如,Tan 等人,2021)、深度神经网络和近似近邻搜索广告(例如,Fan 等人,2019 ;Fei 等人,2021 )、大规模 CTR 模型的 GPU 架构(例如,Zhao 等人,2022a)、另见媒体报道 (www.nextplatform.com/2021/06/25/a-look-at-baidus-industrial-scale-gpu-training-architecture)、广告 CTR 模型压缩(例如,Xu 等人,2021 )、AI 模型安全(例如,Zhao 等人,2022b)、隐私、理论等,以及机器学习在自然语言处理、知识图和视觉中的应用。
尽管,深度神经网络取得了广泛的成功,但作者发现增强树算法在实践中仍然非常有用,例如搜索结果排名、股价预测、金融风险模型等。例如,作者在百度的输入法编辑器(IME)使用了增强树算法,并在手机上部署了树模型(Wang 等人,2020)。根据作者自己的经验,发现增强树算法非常适合具有少于 10000 个特征和少于一亿个训练样本的预测任务。对于使用具有数千亿训练样本的极高维稀疏数据的应用(例如广告 CTR 预估),通常深度神经网络更方便或更有效。
正如最近一篇关于决策树综述的论文(Fan 和 Li,2020)所总结的那样,在过去 15 年左右的时间里,多种实现技术提升了增强树算法的精度和效率,包括:
作者意识到这种差异可能是由于在实现特征分箱过程中的差异造成的。李等人(2007)设计了一种过于简单的定长分箱方法,而 LightGBM 和 XGBoost 似乎使用了更精细的处理。也许与直觉相反,实验表明,李等人(2007)中非常简单的分箱方法在测试的数据集上产生了更准确的结果。
因此,在本报告中,首先描述了 ABC-Boost 包中使用的简单分箱方法,然后演示了如何使用 ABC-Boost 进行回归、二分类和多分类任务。对于每项任务,作者还报告了基于 2022 年 6 月最新版本的 LightGBM 和 XGBoost 的实验结果。
特征预处理固定长度的分箱方法
回归树(Brieman 等人,1983)是分类、回归和排序任务的基础构建模块。树的思想是基于一些“增益”标准以轴对齐的方式递归划分数据点,并报告最终(子划分)区域中数据点的平均(或加权平均)响应作为预测值。子划分的区域作为一个树来组织或者查看,叶节点对应于最终的子划分区域。
因此,一项关键任务是计算每个特征的最佳分割点,并通过将当前节点中的数据点分成两部分来选择最佳特征(即增益最大的特征)来进行实际分割。该过程递归继续,直到满足某些停止标准。在李等人(2007)之前,典型的树实现首先根据特征值对每个维度的数据点进行排序,并需要在分割后跟踪数据点。如图 1 所示,李等人(2007)首先将特征值量化(分箱)为整数,然后按照自然顺序排序。这个技巧大大简化了实现。如果分箱总数不太大,可以使程序更高效。图 1 中的分箱也适用于数据分布,因为它仅在有数据的地方分配分箱值。
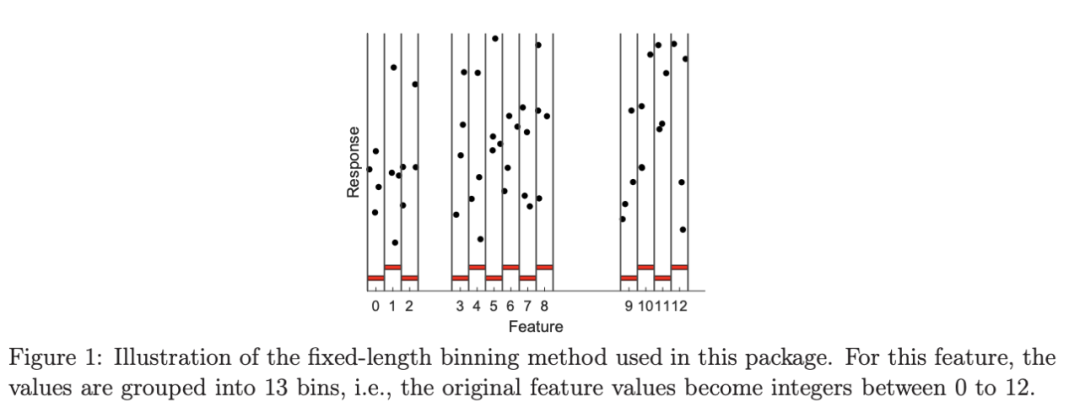
如以下 matlab 代码所示,分箱方法非常简单:首先从非常小的初始分箱长度开始(例如,10^−10) ,预先指定最大的分箱参数,比如 128 或者 1024。对于每个特征,根据特征值对数据点进行排序。将分箱编号从最小到最大分配给数据点,只要有数据点,就一直分配,直到所需的分箱数量超过 MaxBin。然后通过加倍分箱长度来重新开始。
这种分箱程序有许多明显的优点。它非常简单,易于实现。它自适应数据分布。此处理不会影响已排序类别变量的特征。这种处理的缺点也很明显。它绝不是任何意义上的“最优”算法,作者期望它可以在许多方面得到改进。例如,使用固定长度时,如果 MaxBin 设置得太小(如,10),可能会看到较差的精度。另一方面,如果 MaxBin 设置得太小,树算法本身将无法很好地工作。如本报告后面的实验所示,这种极其简单的分箱方法对树表现非常好。作者提供了 matlab 代码,以帮助读者更好地理解该过程,并帮助研究人员改进其分箱算法(和树算法平台)。


总之,这种看似非常简单(固定长度)的分箱算法能适用于增强树方法,可能有两个主要原因:
实际上,作者建议将 MaxBin=100(或 128)设置为开始点。如果精度不令人满意,可以逐渐将其增加到 MaxBin=1000(或 1024)。根据作者的经验,当 MaxBin 大于 1000 时,很难观察到明显更好的精度。
在接下来的三节中,将介绍使用 Fast ABC-Boost 软件包进行回归、二分类和多分类的实验结果。通过将 MaxBin 从 10 更改为 10^4,将结果与 LightGBM 和 XGBoost 进行比较,以说明 MaxBin 对精度的影响。此外,作者观察到,一旦启用多线程,结果变得不确定,尽管随机变化通常不会太大。为了严格确保确定性结果(用于清晰的比较),作者将所有实验作为单线程运行。
Lp 回归
读者请参阅关于 Lp 增强回归的详细报告(Li and Zhao,2022c)。一个训练数据集{yi,xi}(i=1,n),其中 n 是样本数,xi 是第 i 个特征,yi 是第 i 个标签。Lp 回归的目标是建立模型 F(x),以最小化 Lp 损失:

使用“加法模型”(Friedman 等人,2000;Friedman,2001),假设 F 是 M 项的总和:
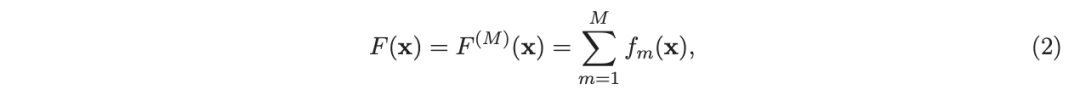
其中,基学习器 fm(x) 是一棵回归树,以分段贪婪的方式从数据中学习。根据 Friedman 等人(2000)的想法,在每次增强迭代中,通过加权最小二乘法拟合 fm,响应值{zi}和权重{wi}:
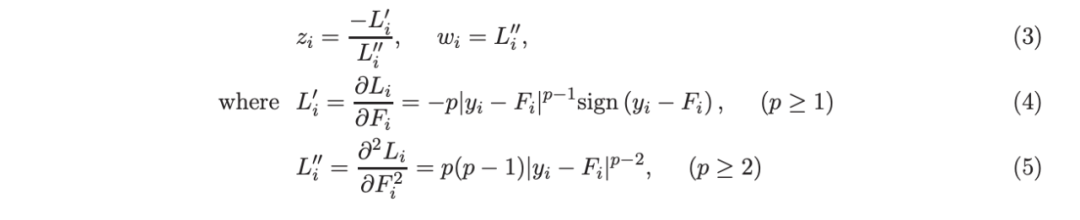
李(2010b)推导了使用响应值{zi}和权重{wi}建立回归树时,确定分裂位置所需的相应增益公式。历史上,基于加权最小二乘法的增强方法被认为存在数值问题(Friedman 等人,2000,2008),因此后来 Friedman(2001)提出仅使用一阶导数拟合树,即,
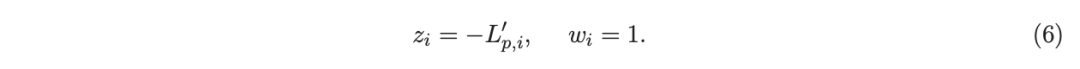
现在很清楚,如李(2010b)所示,可以推导出使用二阶信息计算增益的显式的和数值稳定 / 鲁棒的公式。
基于二阶信息的树分裂准则
考虑一个具有 N 个数据点和一个特定特征的树节点。权重 wi 和响应值 zi,i=1 到 N。已经根据特征值的排序顺序对数据点进行了排序。树分裂过程是查找索引 s,1≤ s<N,因此如果在 s 处分割,加权平方误差(SE)减少得最多。也就是说,寻求 s 最大化:

这个过程在数值上是鲁棒、稳定的,因为,不需要直接计算响应值 zi=-Li’//Li’’,它可以(并且应该)很容易地接近无穷大。由于原始 LogitBoost(Friedman 等人,2000)使用了单个响应值 zi=-Li’//Li’’,因此该过程被认为存在数值问题,这是 Friedman(2001)仅使用一阶导数构建树的动机之一。因此增益公式成为:
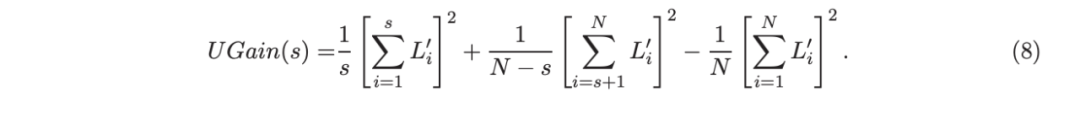
Lp 增强算法
算法 1 描述了 Lp 增强回归树使用的分裂增益公式(7)(对于 p≥ 2) 或树分裂增益公式(8)(对于 1≤ p<2)。注意,在构建树之后,终端节点的值通过以下公式计算:
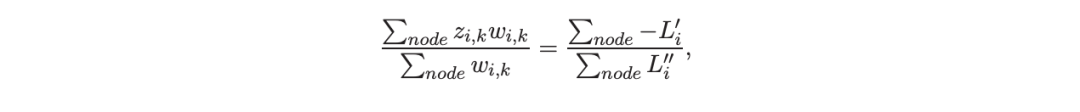

这解释了算法 1 的第 5 行。当 1≤ p<2,作者遵循 Friedman(2001),使用一阶导数建立具有分裂增益公式(8)的树,并将终端节点更新为
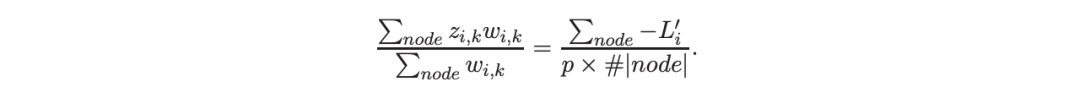
实验
遵循上的说明,用户可以安装 Fast ABC-Boost 软件包。假设可执行文件位于当前目录,数据集位于“data/”目录。“comp-cpu”数据集有 libsvm 和 csv 两种格式,有 4096 个训练样本和 4096 个测试样本。在终端,执行以下命令
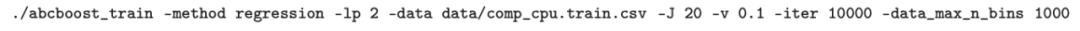
建立一个 L2 回归增强模型,J=20 个叶节点,ν=0.1 收缩率,最多迭代 10000 次。最大分箱数(MaxBin)设置为 1000。作者采用保守的早期停止标准,在 Lp 损失低于以下值后让程序退出
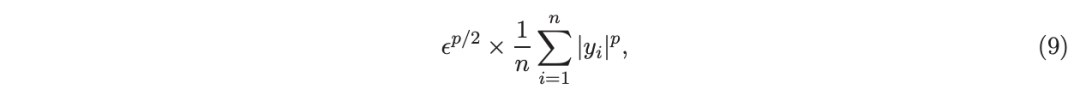
其中ε默认为 10^5。在本例中,程序在 933 次迭代后退出(而不是 10000 次迭代)。在训练后,将在当前目录中创建两个文件:

为了在测试数据集上测试训练后的模型,运行

它会生成另外两个(文本)文件来存储测试结果:

.testlog 文件记录了测试损失和其他信息。“.prediction”存储最终(或指定)迭代中所有测试样本的回归预测值。
用参数 J∈ {6, 10, 20}, ν ∈ {0.06,0.1,0.2},p 从 1 到 10,MaxBin 从 10 到 10^4 进行实验。图 2 绘制了每个 MaxBin 值的最佳(在所有参数和迭代中)测试 MSE。在每个面板上,实心曲线绘制 L2 回归的最佳测试 MSE 和 Lp 回归的虚线曲线(在最佳 p 处)。右面板是左面板的放大版本,重点放在 100 到 10^4 的 MaxBin 上。对于这个数据集,使用 MaxBin=1000 可以获得很好的结果,而使用较大的 MaxBin 值不会产生更好的结果。
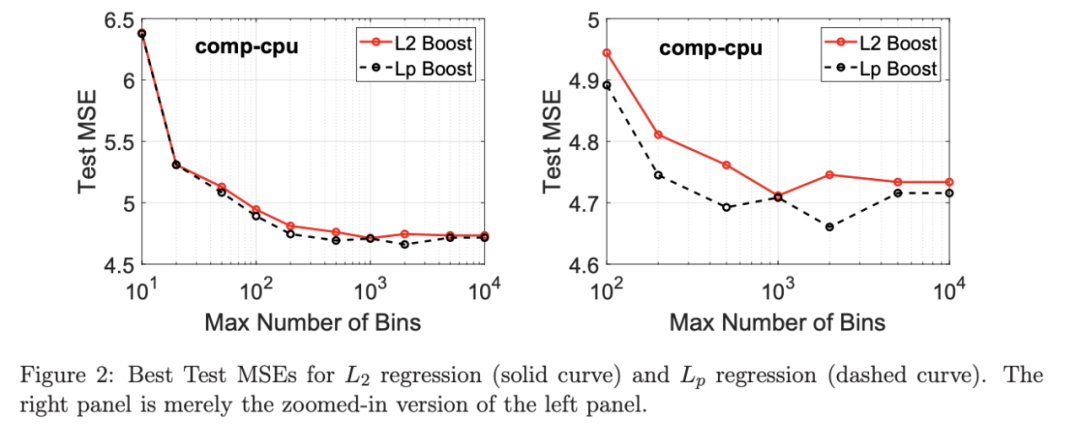
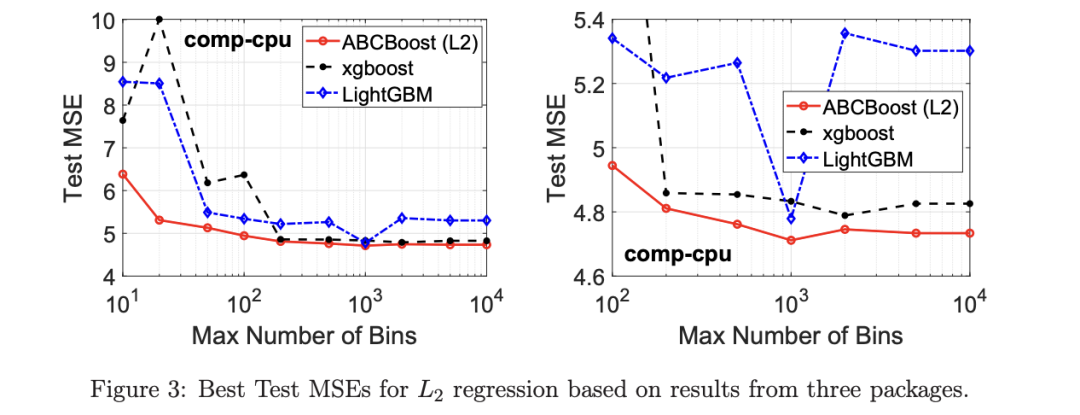
图 3 绘制了所有三个包的 L2 回归的最佳测试 MSEs:ABC-Boost(L2)、XGBoost 和 LightGBM,MaxBin 范围为 10 到 10^4。同样,右面板只是左面板的放大版本。当然,如图 2 所示,ABC-Boost 将能够通过使用 p≠2 的 Lp 回归实现更低的 MSE。
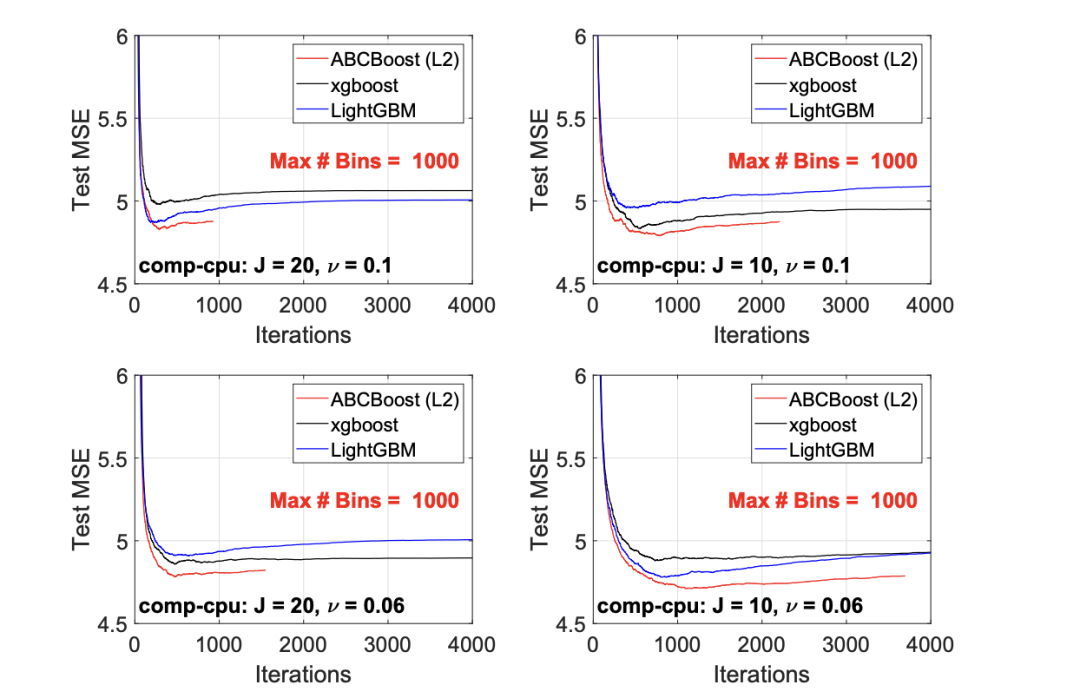
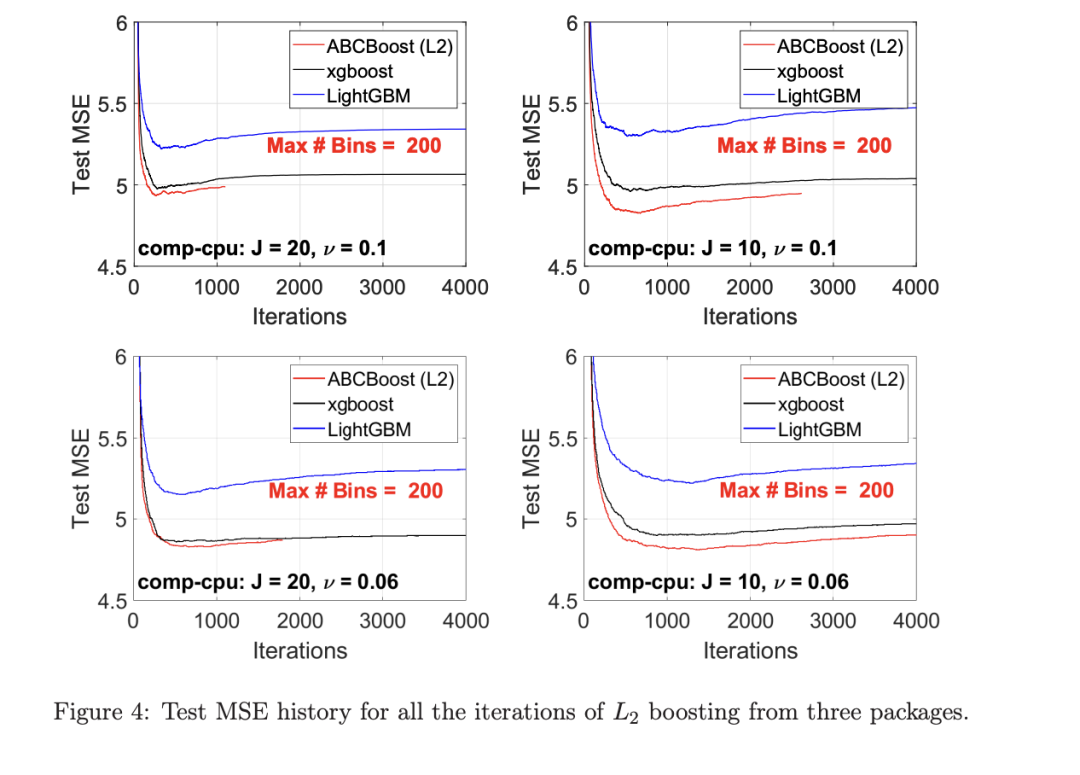
最后,图 4 绘制了所有迭代的测试 L2 MSEs,在一组特定的参数 J、ν和 MaxBin 下。注意,ABC-Boost 包在等式(9)中设置了保守停止标准。
使用鲁棒 LogitBoost 分类
同样,用{yi,xi}(i=1,n) 表示训练数据集,其中 n 是训练样本数,xi 是第 i 个特征向量,yi∈ {0,1,2,…,K− 1} 是第 i 类标签,其中 K=2 表示二分类,K≥ 3 表示多类分类。假设类概率 p(i,k) 为
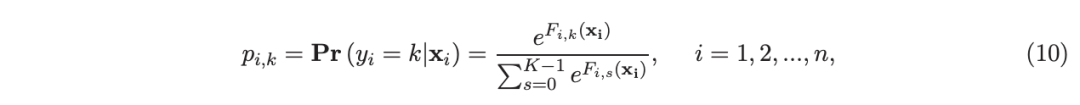
其中 F 是 M 项的函数:
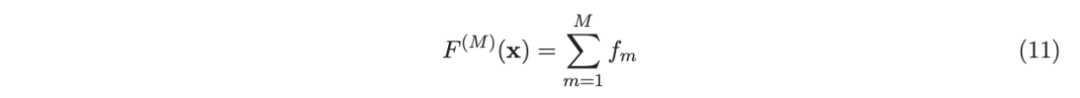
其中,基学习器 fm 是一棵回归树,通过最小化负对数似然损失进行训练:
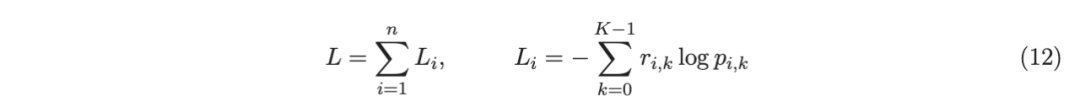
其中,如果 yi=k,则 r(i,k)=1,否则,则 r(i,k)=0。优化过程需要损失函数(12)的前两个导数,分别对应于函数值 F(i,k),如下所示:
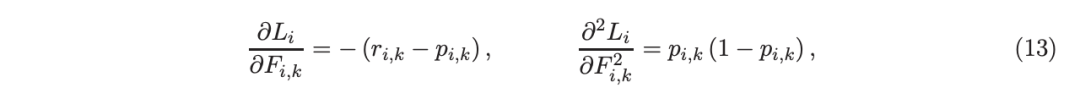
这些是教科书中的标准结果。
基于二阶信息的树分裂准则
再次,考虑具有 N 个权重 wi 和 N 个响应值 zi,i=1 到 N 的节点,假设其根据相应特征值的排序顺序排序。树分裂过程寻求 t 最大化
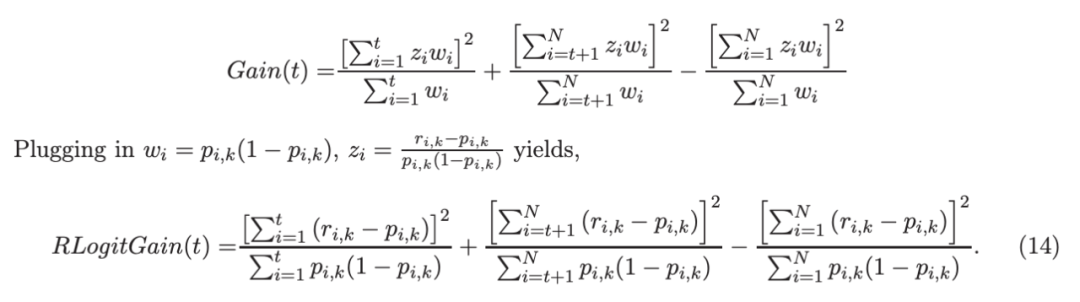
因为计算涉及∑p(i,k)(1− p(i,k) 作为一个组,该程序在数值上是鲁棒、稳定的。这解决了 Friedman 等人(2000)的担忧;Friedman(2001);Friedman 等人(2008 年)。相比之下,MART(Friedman,2001)使用一阶导数来构造树,即,
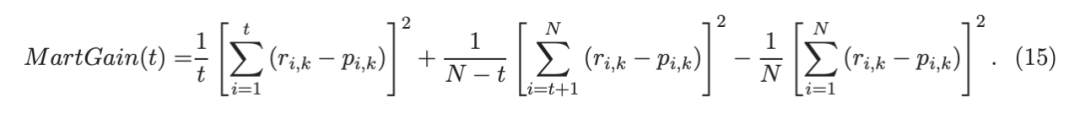

算法 2 使用等式(14)中的树分裂增益公式描述鲁棒的 LogitBoost。注意,在构建树之后,终端节点的值通过以下公式计算:
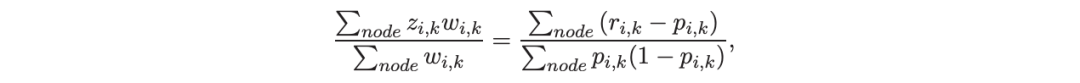
这解释了算法 2 的第 5 行。对于 MART(Friedman,2001),该算法几乎与算法 2 相同,除了第 4 行,MART 使用树分裂增益公式,等式(15)。
注意,对于二分类(即 K=2),只需要在每次迭代中构建一棵树。
二分类实验
二分类数据集“ijcnn1”包含 49990 个训练样本和 91701 个测试样本,可在~cjlin/libsvmtools/dataset/binary.html查看。这个在一次比赛中使用了该数据集,获得冠军的是 LIBSVM(核 SVM),测试误差为 1293 个(在 91701 个测试样本中)。
再次在终端发出以下命令

使用 J=20 个叶节点、ν=0.1 收缩率和 M=10000 次迭代,MaxBin=1000,使用“鲁棒 LogitBoost”算法训练二分类模型。创建两个文件:

打印出“.trainlog”文件的前 3 行和后 3 行:

其中第二列是训练损失,第三列是训练误差。同样,为了确保输出确定性结果,使用单线程训练所有场景。在这里,作者想强调的是,由于潜在的有利随机效应,多线程程序可能输出更好(但不确定)的结果。
下一个命令

输出测试结果

.testlog 文件的最后 10 行如下所示:

其中第三列记录了测试错误。回想一下,LIBSVM 的最佳结果是 1293。注意,在 Li(2010b)的附录中,也给出了在 ijcnn1 数据集上的实验结果。
图 5 绘制了最佳测试误差,以比较 J∈ {10, 20}的鲁棒 LogitBoost 和 MART, ν ∈ {0.06,0.1},M=10000。给出了关于 MaxBin(最大分箱数)的结果,以说明分箱对分类错误的影响。事实上,当 MaxBin 设置为小于 100 时,在该软件包中实现的简单固定长度分箱算法的精度并不好。同样,这是意料之中的。
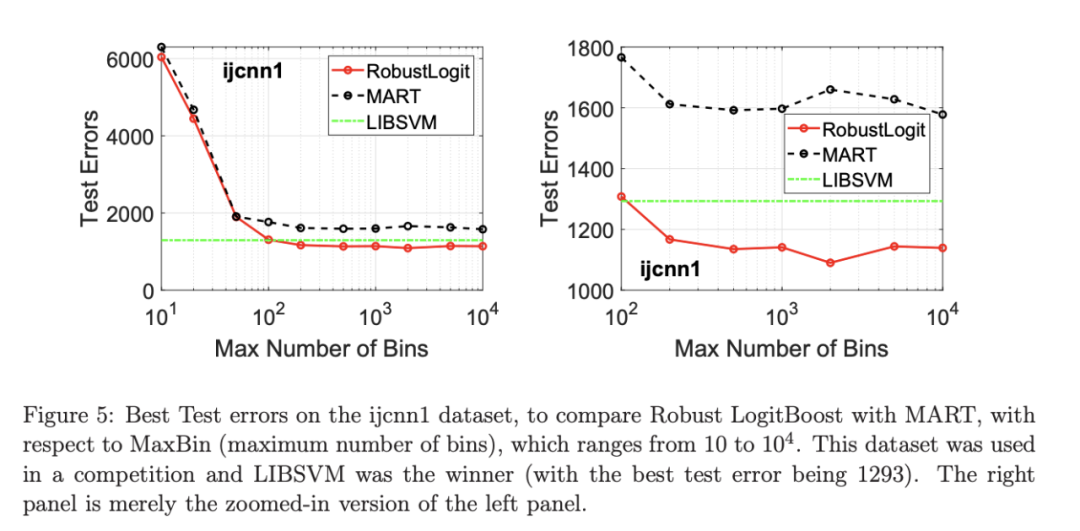
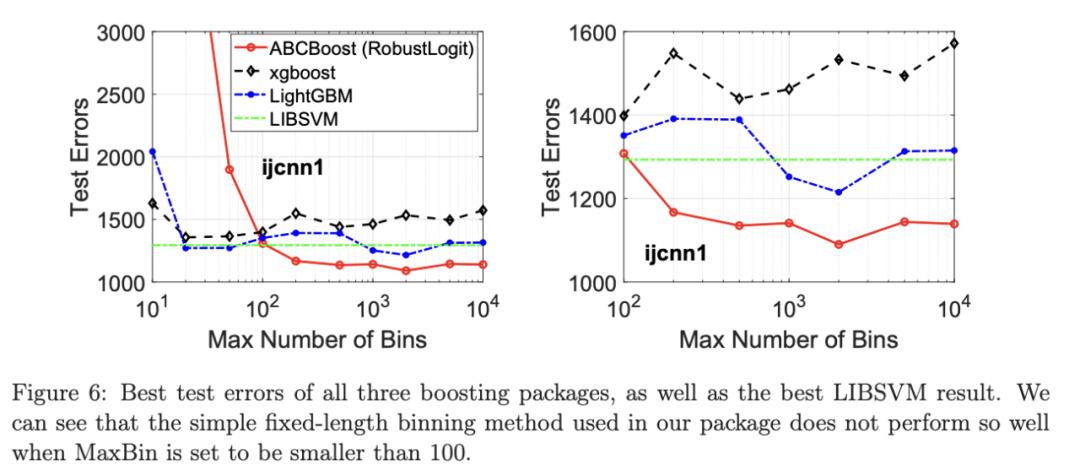
图 6 在相同的 MaxBin 值下比较了鲁棒 LogitBoost 与 XGBoost 和 LightGBM。显然,当 MaxBin 设置为小于 100 时,在作者的包中实现的简单固定长度分箱方法的精度并不好。另一方面,在选择远大于 100 的 MaxBin 处获得最佳(最低)误差(事实上,该数据集为 2000)。
虽然,确实希望有相当大的空间来改进简单(固定长度)的分箱算法,但作者也承认,在使用这种分箱方案大约 15 年后,还没有找到一种普遍(或非常)好的算法。
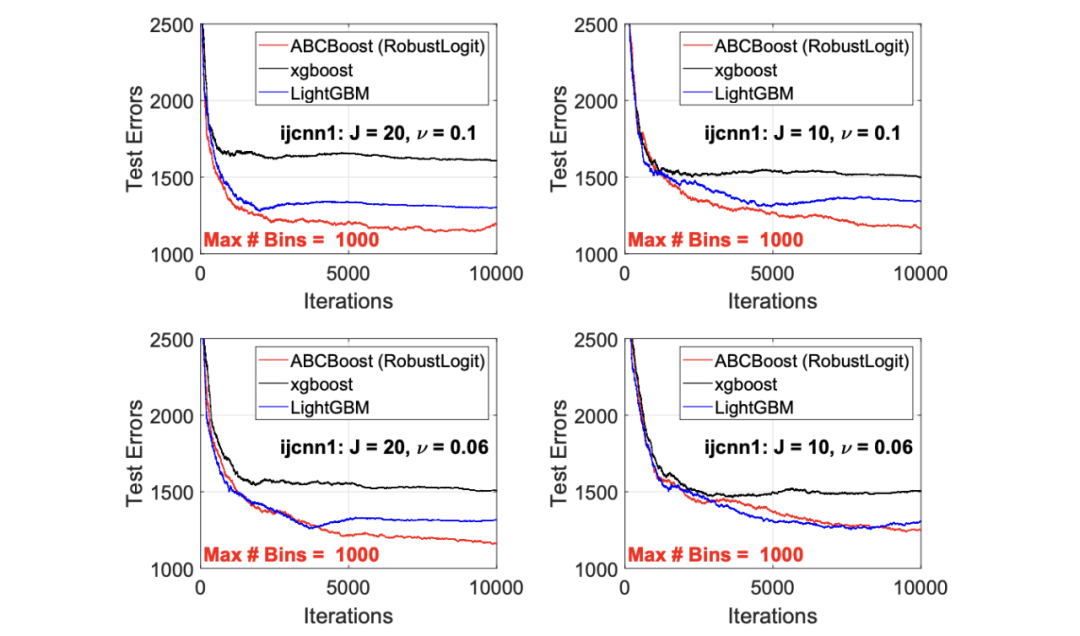
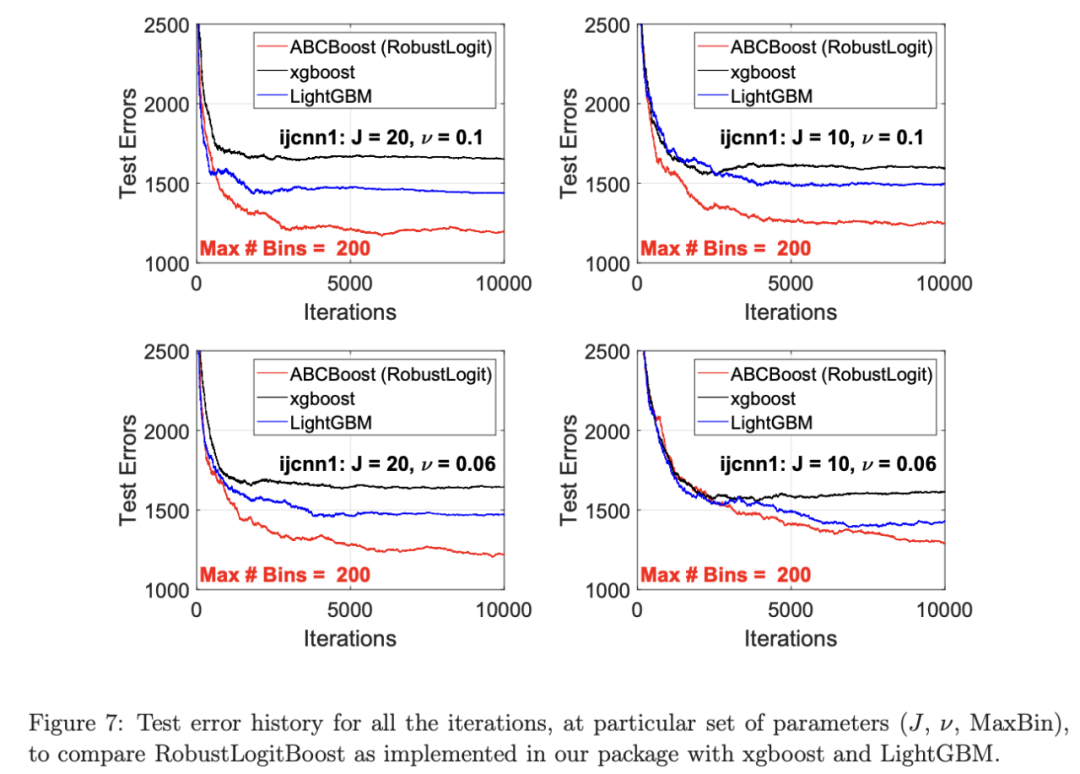
最后,在图 7 中,绘制了每组参数(J,ν,MaxBin)的所有 M=10000 次迭代的测试误差历史,以比较 RobustLogitBoost 与 XGBoost 和 LightGBM。希望从图中可以清楚地看出,从业者可能希望重新回顾这个简单的分箱方法,以进一步更好地理解为什么它工作得如此好,并进一步提高其精度。
用于多分类的 ABC-Boost
“自适应基类增强”(ABC-Boost)的思想起源于(Li,2008),其中将多类逻辑回归的经典(教科书)导数重写为:
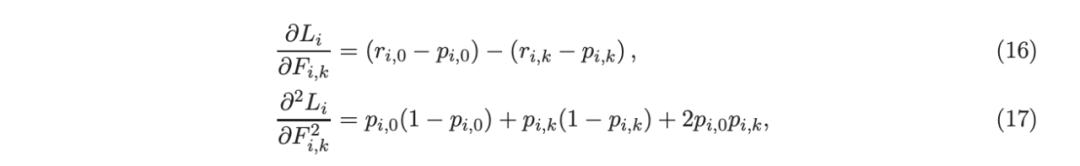
这里,记作,
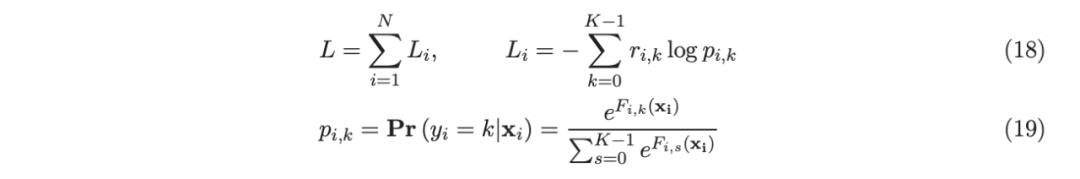
在上面,假设类 0 是“基类”,并对 Fi 值使用“sum-to-zero”约束。在实际实现中,需要在每次迭代中识别基类。
如 Li(2009,2010b)所示,“穷举搜索”策略在准确性方面效果良好,但效率极低。Li(2008)的未发表技术报告提出了“worst-class”搜索策略,而 Li(2010a)的另一份未发表报告提出了“gap”策略。最近,Li 和 Zhao(2022a)通过引入三个参数开发了一个统一的框架来实现“快速 ABC-Boost”:(i)“搜索”参数 s 限制了对 s-worst 类中基类的搜索。(ii)“gap”参数 g 表示仅在每个 g+1 迭代中进行基类搜索。(iii)最后“预热”参数 w 指定搜索仅在为 w 迭代训练了鲁棒 LogitBoost 或 MART 之后开始。
算法 3 总结了快速 ABC-Boost 的统一框架。虽然它引入了其他参数(s、g、w),但好消息是,在大多数情况下,精度对这些参数并不敏感。事实上,Li(2008)最初提出的“worst-class”策略已经非常有效,尽管在某些情况下可能会导致“灾难性失败”。在某种意义上,引入这些参数(s、g、w)主要是为了避免“灾难性失败”。
在算法 3 中,ABC-RobustLogitBoost 中树分裂的增益公式类似于(14):
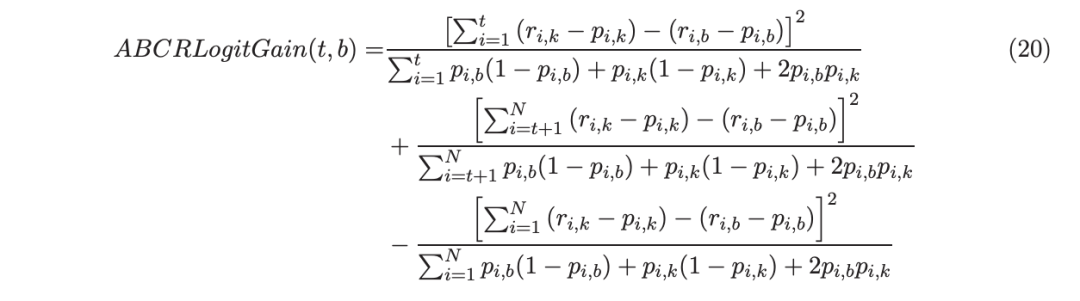

使用 UCI“covtype”数据集进行演示。该数据集包含 581012 个样本,将其分为一半用于训练 / 测试。这是一个 7 个类的分类问题。在实验中,假设 J=20,ν=0.1,M=1000。执行以下命令:
./abcboost_train -method abcrobustlogit -data>
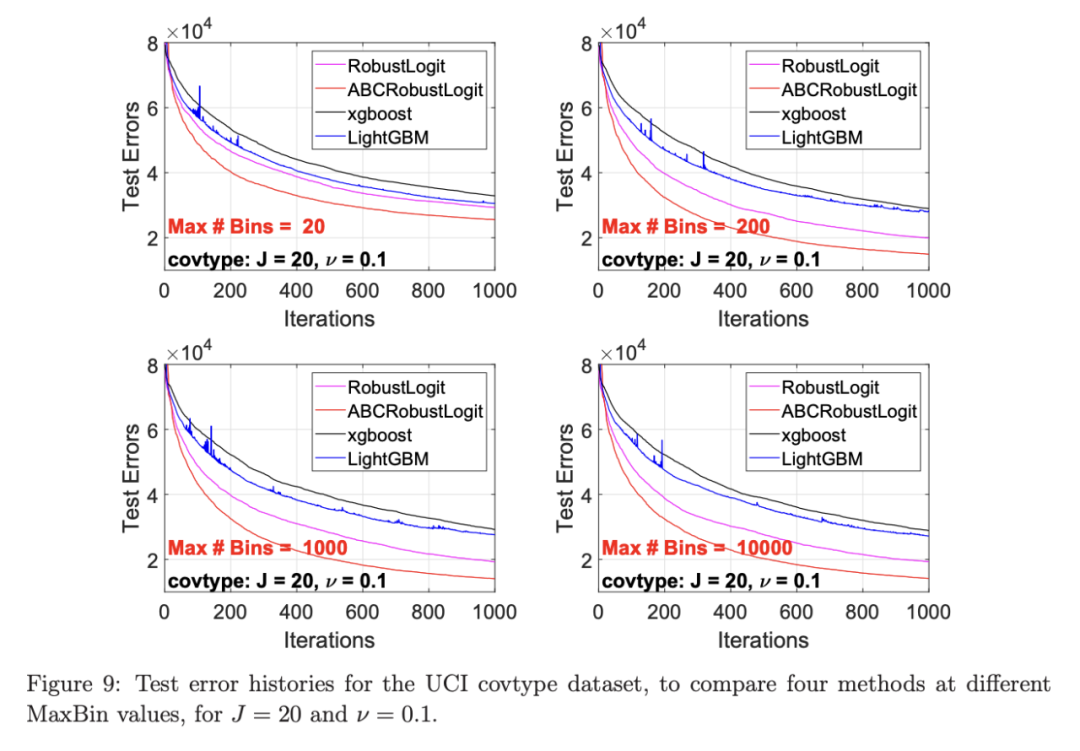
训练并测试 s=2 和 g=10 的“ABC RobustLogitBoost”。当然,也可以像算法 2 那样训练规则的鲁棒 LogitBoost。图 8 比较了四种不同方法的测试误差:Robust LogitBoost、ABC Robust LogitBoost、XGBoost 和 LightGBM,用于分箱参数 MaxBin 从 10 到 10^4。

图 8 显示,当 MaxBin=10 时,在作者的包中实现的简单固定长度分箱方案表现不佳。这是意料之中的。对于这个多分类任务,很明显,“ABC 鲁棒 LogitBoost”大大改进了“鲁棒 LogitBoost”。
最后,图 9 绘制了四种方法的测试误差历史。

结论
十年前(或更早),作者完成了 Li 等人(2007)在增强技术和树模型方面的贡献;Li(2008、2009、2010a、b),这产生了很多有趣讨论(参见示例讨论)年),并推动了使用(i)特征组合的流行增强树平台的开发;(ii)树分裂的二阶增益公式,作为标准实现。然后,作者将兴趣转移到其他主题,包括深度神经网络和商业搜索引擎的计算广告;虽然作者在商业广告应用中广泛使用深度神经网络,但增强树在工业中仍然非常流行。作者自己的“经验法则”是,如果应用程序具有少于 10000 个(手工制作或预生成的)特征和少于一亿个训练样本,则应首先尝试增强树。
注意到,“自适应基类提升”(ABC boost)尚未成为流行的提升树平台的一部分。这可能是因为在正式发表的论文(Li,2009,2010b)中,作者只报告了计算成本高昂的穷举搜索策略,这可能会阻止从业者尝试 ABC-Boost。因此,作者决定发布“快速 ABC-Boost”,这实际上是 Li 和 Zhao(2022a)总结的过去 15 年努力的结果。
最后,值得一提的是,在作者所有关于增强技术和树模型的论文中,包括 Li 等人(2007),在实现过程中,始终使用“最佳优先”的树生长策略。Li 是在 2000 年初参加弗里德曼教授的课堂(并担任他的助教)时产生这个想法的。见本教程第 76-77 页。这是作者在康奈尔大学和罗格斯大学工作期间编译的课件。
论文原文链接:
开源代码连接:





