手机导航是手机地图中非常重要的功能。偏航检测(车辆是否偏离规划路线)是手机导航中至关重要的任务。传统偏航检测方法通过检测车辆的位置(低精度)或运动方向是否偏离规划路线,判断车辆是否偏航。
而在高架区域(包含高架桥和平行辅路)中,识别车辆是否偏航是非常困难的。因此,识别车辆是否在高架上行驶,能够极大地提升高架区域的偏航检测效果。
在本文中, 高德地图在线引擎中心提出了高架道路网络(Elevated Road Network,ERNet),一个轻量级且真正工业级别的神经网络模型,用于解决高架区域中的偏航检测难题 。
具体而言,对于同一组高架道路片段和平行辅路片段,ERNet 以 4 种高语义级别的特征作为输入,学习得到两个 10 维的道路描述子向量(A 和 B)。在推断阶段,对于车辆的一个位置,ERNet 预测一个 10 维的 embedding 向量(C)。最后通过比较 ||A-C|| 和 ||B-C||,并结合置信度约束(confidence constraint),我们能够识别出车辆是否在高架上行驶。
在大量的实验中,ERNet 取得了很好的效果。目前,ERNet 已经在高德地图手机客户端上线,支持北京、上海和广州三个城市的高架区域偏航检测。
序言
手机导航是手机地图的核心功能。在高德地图(中国最流行的手机地图 APP),人们每天请求海量的导航服务。在一次旅程中,如果车辆偏离了导航服务为其推荐的最佳规划路线,手机导航系统需要及时地检测出这一偏航事件,并规划一条新的路线。
传统的偏航检测方法(在手机地图中)主要依赖 GNSS 系统提供的车辆位置和行驶方向信息。一般地,如果车辆的位置(或方向)距离规划路线连续地超过 T_d 米或(T_a 角度),一次偏航事件可以被检测出,如下图 1 所示。

图 1:传统偏航检测方法可以在中间图(距离超出 T_d)和右侧图(角度超过 T_a)检测出偏航事件。
在中国,高架道路作为城市快速交通的关键组成部分,被大量建造。尤其在上海,有超过 622km 的高架道路,几乎覆盖全城。在高架道路附近,GNSS 系统提供的位置和行驶方向精度较低(可能误差会超过 20 米,如下图 2 所示)。
因此 T_d 和 T_a 必须足够大,否则偏航检测方法可能会误报偏航。这就导致在高架区域(高架桥附近存在较近的平行辅路)中,传统的偏航检测方法无法正确检测出偏航事件。如果我们能够正确识别出车辆是否在高架桥上(高架道路识别),势必会给偏航检测方法带来质的提升。
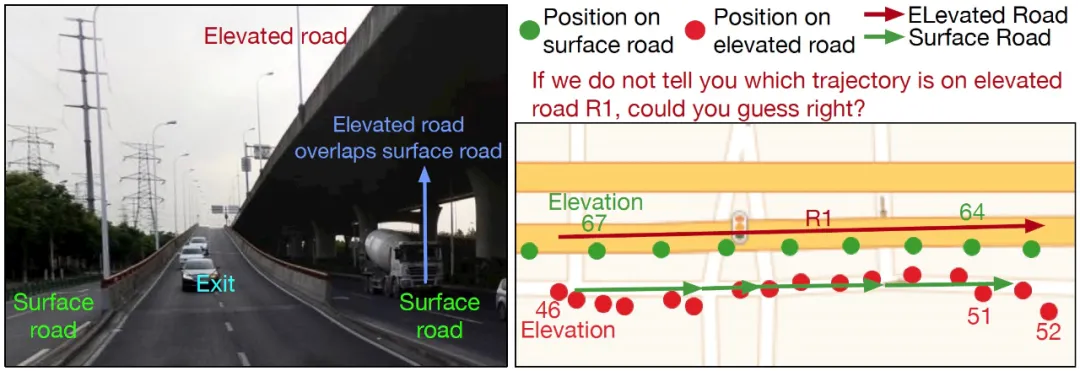
图 2:左子图:高架道路(Elevated road)跟旁边的辅路(Surface road)距离较近,而且方向平行。右子图:两条轨迹存在较大的水平位置误差。红色轨迹来自行驶在高架桥 R1 的车辆,但是其位置却落在辅路上。同样地,绿色轨迹来自行驶在辅路上的车辆,其位置落在高架桥上。需要注意的是,红色轨迹的位置(高架桥是水平的,没有高度差)的高度取值范围从 46 米到 52 米。而且,红色轨迹的高度取值小于绿色轨迹(真实在辅路上的位置)的高度取值。
现有高架状态识别方法的局限
目前存在的高架状态识别方法大致可以分为三类: 地图匹配方法、高程计算方法和特征识别方法 。
地图匹配方法使用 Map-Matching 技术[9, 10, 14],考虑时序的车辆位置、方向、路网等信息,在路网中为车辆运行的轨迹选取合适的道路。这种方法在一般场景中工作良好,但是在高架区域表现糟糕。这主要是由于高架桥与平行辅路的方向一致,且距离很近,而地图匹配方法依赖的车辆位置和方向在高架区域精度较低,不足以精确区分轨迹是否在高架桥上。而路网的拓扑信息在高架桥存在较多的出入口时,也无法精确建模,如下图 3 所示。
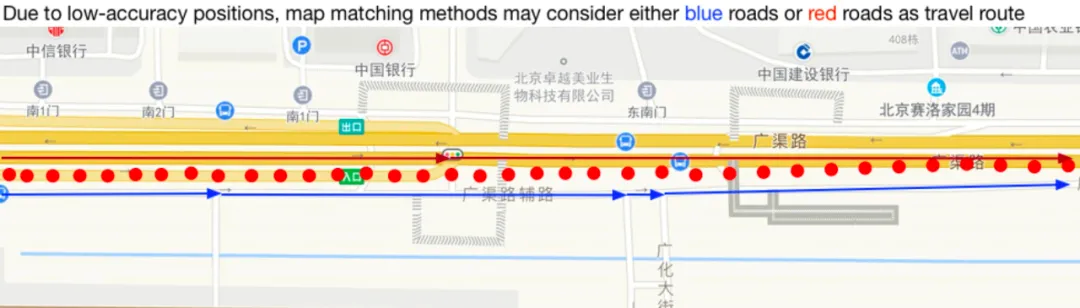
图 3:当路网拓扑信息在高架区域存在出入口时,由于 GNSS 位置精度较低,地图匹配方法很难确认一条轨迹是来自高架桥上行驶的车辆还是来自平行辅路上行驶的车辆。
高程计算方法主要使用高度或高度差信息,例如使用 GNSS 系统提供的高度或使用气压计测量值计算的高度差。不过,GNSS 系统提供的高度信息基本不可用[3](如上图 2 所示)。至于气压计,仅 iPhone 和少数高端的 Android 手机才装备。并且,气压计在车辆窗口打开后,读数非常不稳定(如下图 4 所示)。汽车速度越快,气压计读数越低,测量的高度越高。
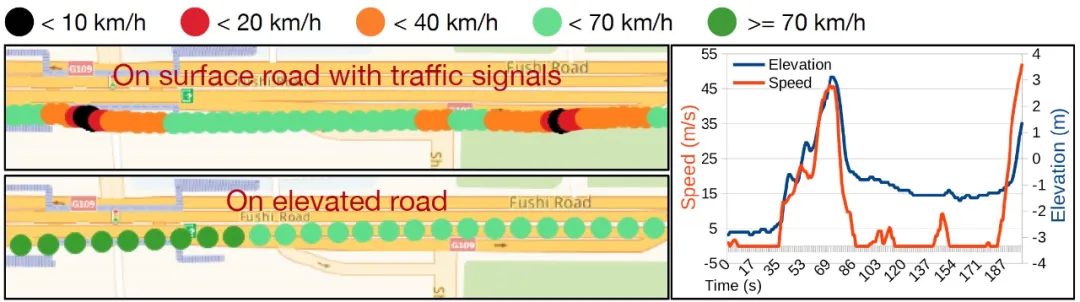
图 4:左子图:一辆车在平行辅路上频繁地加速和减速(上侧),在高架桥上保持较快的速度(下侧);右子图:当车辆窗户打开后,气压计测量的高度变化在平面道路上出现了较大的差异(超过 7 米)。
特征识别方法提取能够区分车辆在高架桥上和桥下的平行辅路行驶的本质差异特征,并将这些特征作为模型(HMM 或分类器)的输入。模型的输出为车辆的状态:行驶在高架桥上和行驶在高架桥下的平行辅路。方法 [2] 使用了非常简单的特征,例如车辆速度的方差、可追踪卫星(GNSS 系统由多颗卫星组成)的数量等。然而,速度和卫星信号可以提供非常有意义的信息,用于捕获车辆行驶在高架桥上和桥下平行辅路的本质差异,见图 4 和图 5。因此更加复杂的特征应该被考虑进来。
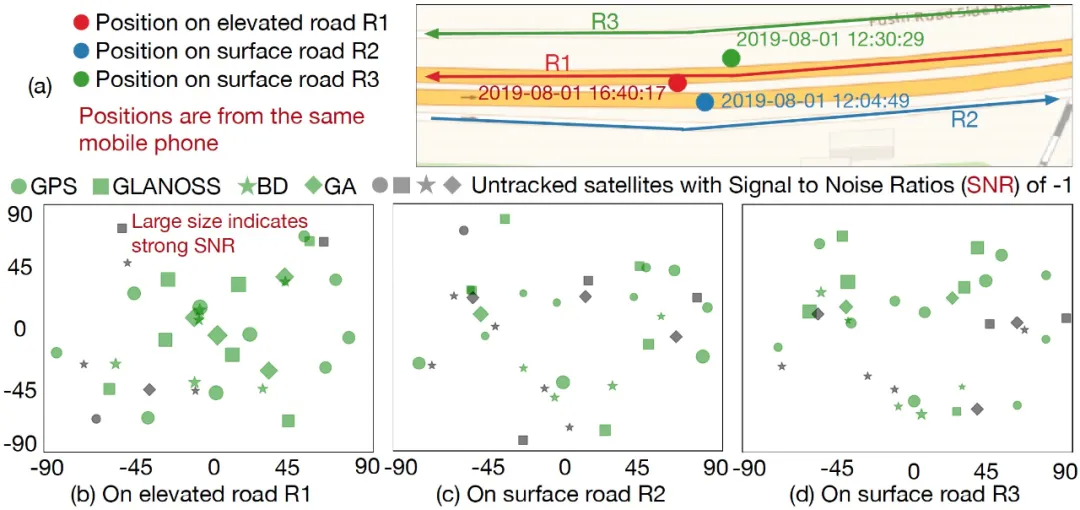
图 5:卫星信号在高架桥上和平行辅路上存在较大差异。(a)三个位置分别在高架桥 R1 上,在平行辅路 R2 和 R3 上。(b)在 R1 上,大多数的卫星信噪比比较强(图标尺寸比较大),有 7 个卫星未被追踪到(无法用来进行 GNSS 定位)。(c)由于 R2 北方被高架桥遮挡,北方的卫星的信噪比比较低,且 12 个卫星未被追踪到。(d)跟(c)非常类似,南侧的卫星的信噪比比较低,且 9 个卫星未被追踪到。
如何设计有效的高架状态识别方法?
为了设计一个有效的高架状态识别方法,我们面临以下三个主要挑战:
近年来,以神经网络为代表的模型在多个任务中取得了极佳的效果,所以有足够的动机去尝试它们。
对于挑战 1,我们更倾向于使用轻量级(层数较少)的神经网络,而不是深度神经网络(有可能取得更佳的实验效果,但是计算代价巨大);
对于挑战 2,我们可以使用车辆在手机导航过程中上传的 GNSS 信息(车辆位置、运动方向,卫星空间位置、卫星信噪比等),设计一个自动标注算法,标注出车辆实际行驶的道路序列。
对于挑战 3,我们需要设计一个有效的特征提取方法来处理卫星信号。此外,在许多局部区域,高架桥下接收的卫星信号和高架桥上接收的卫星信号差异巨大。而在某些局部区域,差异较小。例如,当高架桥下的平行辅路距离高架桥较远时,遮挡情况较弱,因此平行辅路上行驶的车辆也能接收到较强的卫星信号。
而在高楼林立的市区,即使车辆行驶在高架桥上,也会因为受到高楼的遮挡,继而接收到的卫星信号较弱,如下图 6 所示。为了对这些区域差异进行建模,我们可以使用局部编码技术,为每个局部区域编码生成一个维度为 d 的 embedding 向量。
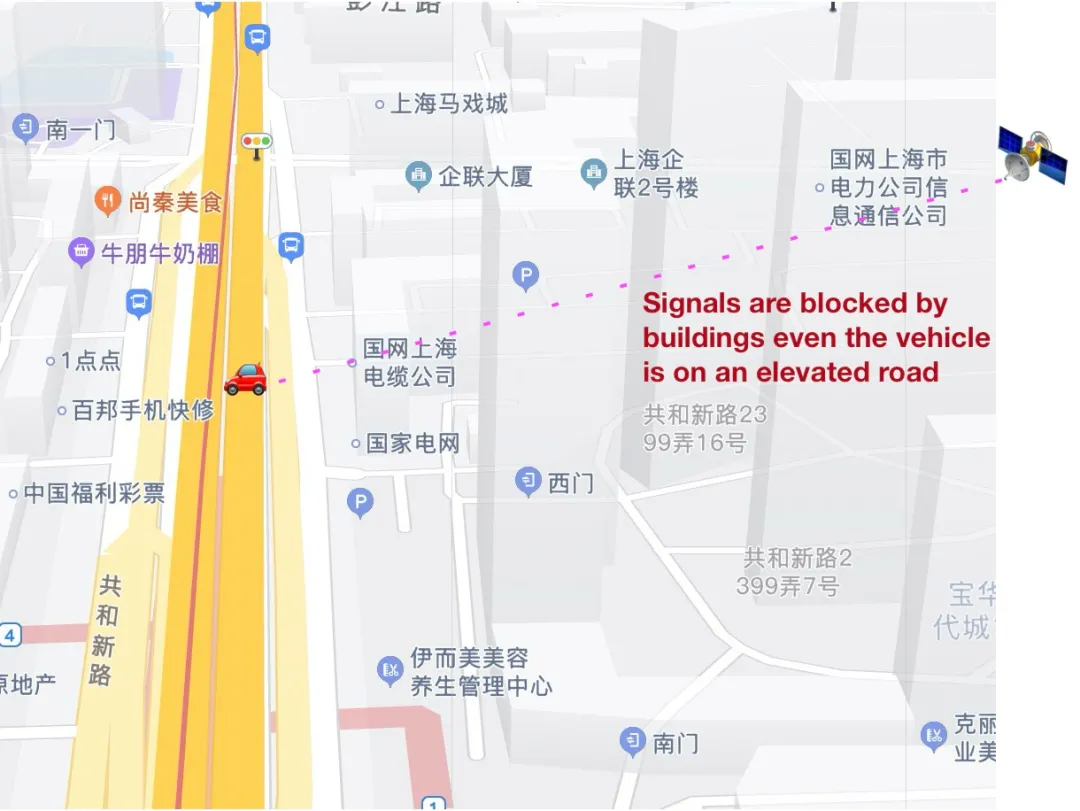
图 6:即使车辆行驶在高架桥上,在某些区域,卫星信号的传输会受到高楼的遮挡,因此车辆内手机接收到的卫星的信噪比和追踪到的卫星个数可能也会比较低(跟桥下行驶的车辆没有明显差异)。
同时,为了学习到有区分性的特征(同类样本在学习到的特征空间距离较近,不同类样本在学习到的特征空间距离较远),一些损失函数,例如 center loss [13],triplet loss [11] 和 triplet-center loss [5] 被提出。使用这些损失函数训练的技术称为 metric learning 技术。
高架道路识别是一个局部问题。对于每一个位置,我们都可以计算出其属于哪个局部区域。我们在学习过程中,只需要确保属于同一个局部区域的不同类别的样本在特征空间上距离较远,同一个布局区域的同类别的样本在特征空间上距离较近。Softmax loss 则要求不同类别的样本都要在特征空间上距离较远,同类别的样本都要在特征空间上距离较近,而不管样本是否属于同一个局部区域。
根据之前的分析,研究者提出了一个特征识别方法。 该方法基于 Elevated Road Network(ERNet),一个轻量级而且真正意义上工业级别的模型,从根本上解决高架道路识别问题 。
ERNet 在一个大的自动标注的训练样本上进行训练,并在一个手工标注的样本集上进行验证和测试。ERNet 输入 4 类高语义的特征,并使用 triplet loss 进行训练。ERNet 为同一个局部区域(我们称之为 group)的高架桥上片段和桥下平行辅路片段各学习一个γ维的道路描述子 A 和 B。在推断阶段,ERNet 为每一个待预测的位置预测一个γ维的特征 embedding C。如果 ||A-C||<||B-C||,则可以简单地认为车辆行驶在高架桥上。
不过为了提升识别的准确率,研究者提出了一个置信度约束的机制。本文同样提出了一个基于 ERNet 的偏航检测方法。
本研究的贡献可以总结为以下四点:
ERNet 模型详解
离线数据处理
在一次旅行中,为了请求导航信息(例如规划路线、交通拥堵信息),手机导航系统会上传 GNSS 信息到我们的地图服务器。因此地图服务器拥有大量的 GNSS 信息和规划路线信息,这些被称为原始数据。
由于研究者希望使用 group embedding 技术,所以需要将原始数据转换为 group 数据。group 数据的每个实例包含:group ID、高架道路距离、GNSS 信息和道路类别。
具体地,研究者首先提炼出车辆真正行驶的路线 travel route,然后将车辆行驶轨迹的每个点投影到 travel route 上计算 group ID、高架道路距离和道路类别。前者他们称为 route refinement,后者称为 group projection。
Route refinement
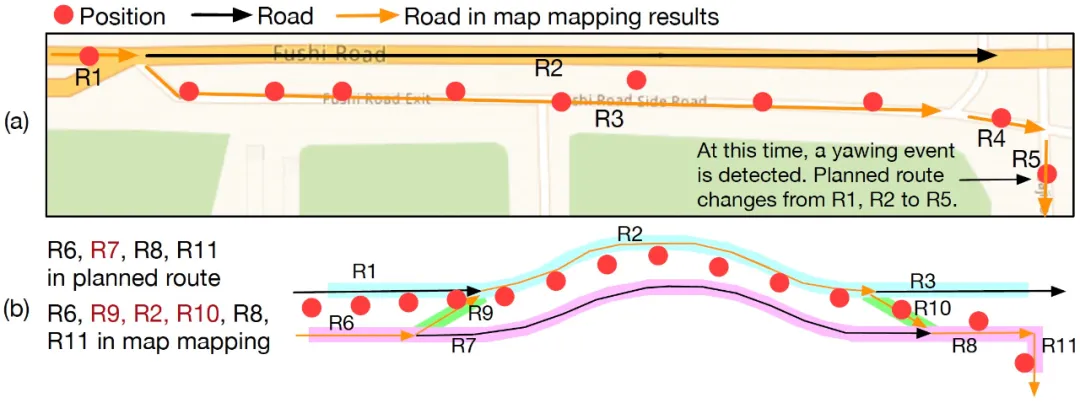
图 7:(a)地图匹配方法将轨迹点匹配到邻近的道路上(黄色道路)。(b)一辆车行驶在 R6、R7、R8 和 R11 上,并没有偏航(规划路线也是如此)。
在一次旅程中,如果车辆偏航,将会有不止一条规划路线。由于 travel route 无法直接合并多个规划路线,如上图 7(a)所示。因此研究者需要提炼出 travel route。
具体地,研究者使用地图匹配方法将一条轨迹的全部位置匹配到附近的道路上,从而得到一组连续的道路,见图 7(a)。由于地图匹配方法使用的是低精度位置,因此匹配道路可能是错误的。例如,图 7(b)中,travel route 实际上包含 R6、R7、R8 和 R11。而地图匹配的结果为 R6、R9、R2、R10 和 R8。其中 R9、R2 和 R10 并不是车辆实际行驶的道路。
在高架区域中,对于平行的高架桥上道路和桥下的平行辅路,如果存在地图匹配道路和规划路线道路不一致的问题,则更倾向于相信规划路线的道路。这主要因为在高架区域,仅有 3% 的车辆会偏航(而地图匹配的错误率要远高于 3%)。例如,图 7(b)中,更愿意相信车辆行驶在规划路线中的 R7 上,而不是地图匹配路线中的 R9、R2 和 R10。当然,相信规划路线会导致大约 3% 的道路并不是车辆真正行驶的道路(相当于训练样本存在 3% 的噪声数据)。不过,这对于神经网络而言,仍然可以训练得到精度较高的模型,只要能够更好地处理过拟合问题。
Group projection
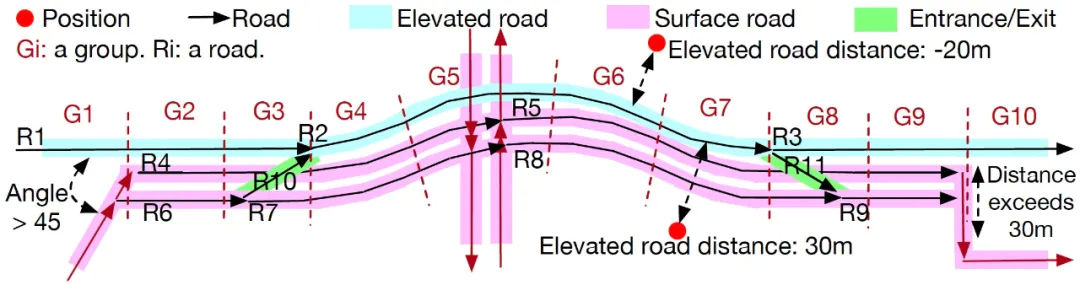
图 8:我们将一条高架道路切分为多个 group。每个 group 的长度接近α米。每个 group 包含一个高架桥片段,和一个或多个平行辅路片段。如果一个 group 内的平行辅路片段到高架桥片段的距离超过 30 米或者夹角大于 45 度,我们舍弃掉这个 group,例如 G1 和 G10。
问题的关键在于如何为每个位置计算其所属的 group。上图 8 显示将一个高架桥切分为多个 group。每个 group 的长度为α。对于一次旅程的轨迹,我们将全部位置顺序的投影到 travel route 上,寻找每个位置最佳的匹配道路,如下图 9 所示。如果最佳匹配道路即为高架道路,那么投影距离即为高架道路距离,投影处对应的 group 即为高位置所属的 group。
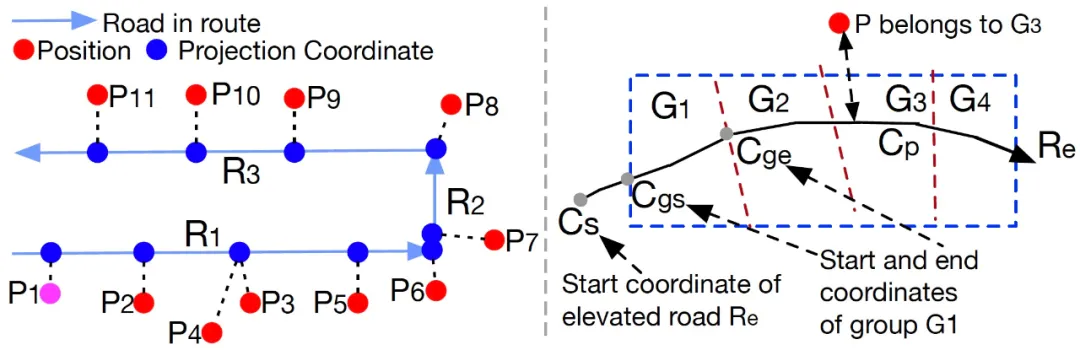
图 9:左子图:位置被顺序地投影到 travel route 上。每个位置匹配到最近的近似平行道路上(道路的方向和运动方向夹角接近)。注意,对于回退位置(例如 P4),研究者将其投影到 P3 投影的道路上;右子图:一个 group 的范围被表示为[Gs,Ge],这里 Gs 或 Ge 指的是 Cs 到 Cgs 或 Cge 的距离。
对于最佳匹配道路为平行辅路的位置,研究者使用一个叫 road map 的结构。road map 的每个实例为平行辅路的 ID 和对应的高架桥道路的 ID。这里对应指的是平行辅路和高架桥是同向而且是临近重叠的。例如,在图 8 中,平行辅路 R6 的对应高架桥道路 ID 为 R1,而平行辅路 R7 对应的高架桥道路 ID 为 R1 和 R2。使用 road map,最佳匹配道路为平行辅路时,我们获取对应的高架桥道路,并将位置投影到高架桥道路上,获得高架道路距离和 group ID。
特征
ERNet 使用 4 类特征:1)卫星平面投影特征(Satellite Plane Projection, SPP);2)group ID;3)高架道路距离;4)序列速度特征。
SPP 特征捕获了卫星信号分布。在高架桥上接收和桥下平行辅路接收的卫星信号分布差异很大,如图 5 所示。group ID 可以提供局部信息。大的高架道路距离表示车辆行驶在距离高架桥较远的平行辅路上(没有卫星信号遮挡)或行驶在距离高架桥较近的平行辅路上(卫星信号遮挡验证,因此位置飘逸严重)。
下图 10(c)显示了序列速度特征的提取方式。尽管每个 bin 长度设置地更小能够提供更丰富的内容信息,用来区分车辆加减速是由于红灯导致还是由于交通拥堵导致。当速度较快时,一些 bin 可能没有位置数据。为了避免这种情况,研究者设置每个 bin 的长度为 30 米(车辆速度低于 108km/h 时,每个 bin 都存在位置数据)。
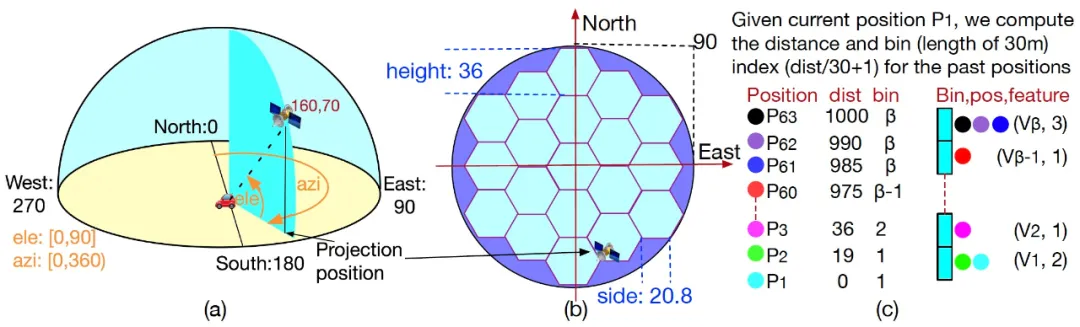
图 10:(a)卫星的空间位置是(160,70),160 是指方位角,70 指俯仰角;(b)卫星的投影平面被切分为 19 个正六边形;(c)时序速度特征包含β个 bin。其中每个 bin 包含属于该 bin 的位置的平均速度和位置的个数。
对于每个位置,我们能够非常容易计算出其所属的 group、高架道路距离和序列速度特征。因此这里重点讨论下 SPP 特征。
具体地,研究者将投影平面切分为 19 个正六边形(图 10(b)所示)。六边形网格切分空间在地图领域经常被使用[12]。卫星的空间位置(azi, ele)对应到投影平面的坐标 p 可以按照如下方式计算:
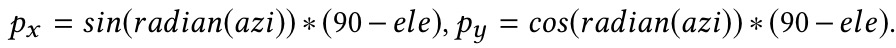
对于每一秒接收到的卫星信号,在每个六边形 H 中,研究者为每类卫星 T 计算 3 维特征:
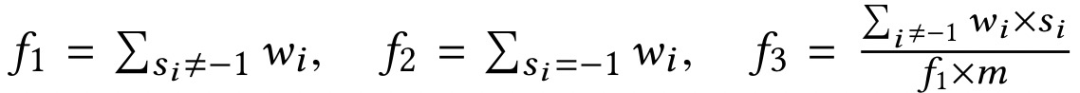
这里 S_i 表示卫星 i 的信噪比(信噪比数值越大,则卫星信号越强)。m 代表手机的 GPS 接收机能够接收到的该类卫星(T)的最大信噪比(可以统计最近 20km 内,该类卫星 T 接收到的最强 SNR)。W_i 是高斯加权,通过如下方式计算:
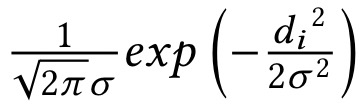
这里是卫星 d_i 的投影坐标 p 到六边形 H 中心的距离。研究者设置σ为六边形边长的 2 倍。
对于一个六边形 H,一个大的 f_1 (f_2) 表示更多可追踪(不可追踪)卫星的投影坐标更接近 H 的中心,这捕获了卫星的位置分布。f_3 是卫星信噪比的加权平均值(使用最大卫星信噪比标准化)。大的 f_3 表示投影坐标靠近 H 中心的卫星的信噪比接近该类卫星的最大信噪比。因此 f3_捕获了卫星的信号强度分布。
由于研究中使用了 4 类卫星,因此 SPP 特征的维度总数为 4*3*19 = 228。SPP 特征是高语义级别的特征而且计算非常高效,因此非常适合手机设备。
网络结构
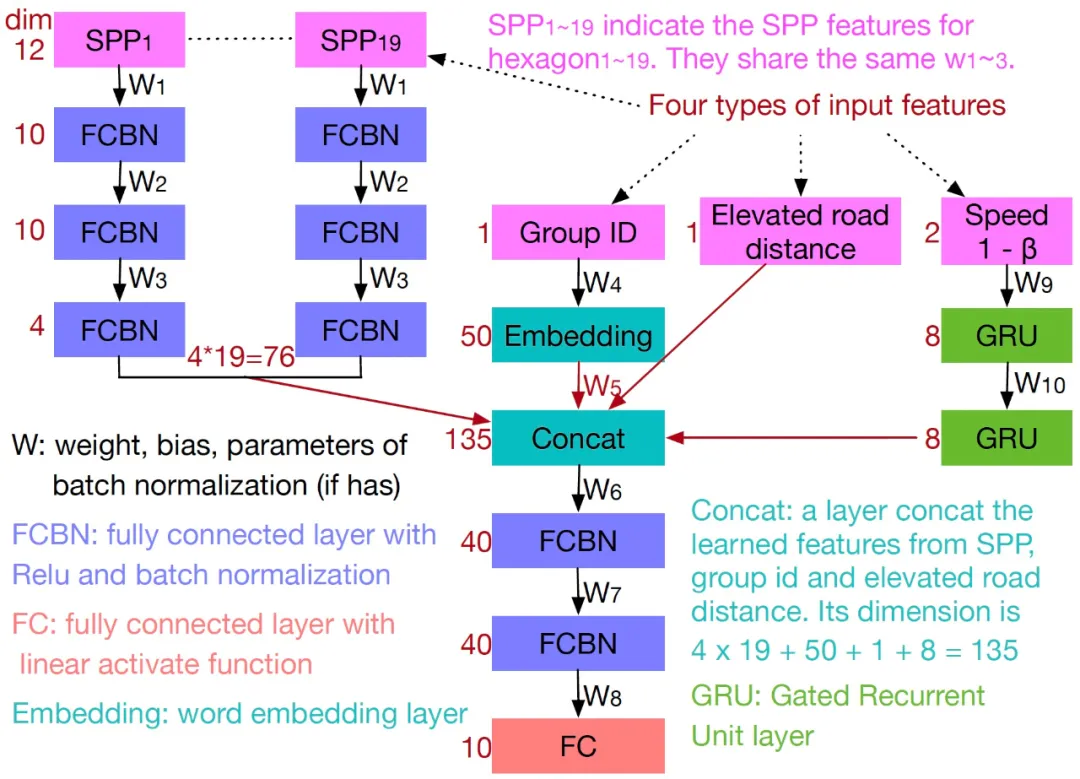
图 11:ERNet 包含 10 个权重层。SPP 特征在不同六边形的特征分量共享 W1、W2 和 W2。
ERNet 被设计为在手机设备上运行的轻量级网络,如上图 11 所示。对于 group ID 特征,研究者使用 group embedding 技术将 group ID 编码为一个 50 维的 embedding 向量。高架道路识别可以直接使用 softmax loss 训练一个二分类模型。
不过,高架道路识别是一个局部问题,可以为每一个待识别的位置计算其所属的局部区域(也就是 group)。因此只有属于同一个 group 的不同类别的样本才需要在特征空间存在区分度,如下图 12 所示。Triplet 和 triplet-center loss 非常适合解决局部问题。

图 12:不像传统的损失函数 Softmax 强制要求所有不同类别的样本在特征空间分开,triplet 和 triplet-center loss 可以做到只要求属于同一个局部区域的不同样本在特征空间分开,因此更适合解决局部问题。
由于在实验中,研究者发现使用 triplet loss 训练的效果比使用 triplet-center loss 训练的效果更好,因此本研究更倾向使用 triplet loss 训练 ERNet。
研究者使用 Batch All [6] 策略在 group 内部构造 triplet 样本。所谓 group 内,指的是任意一个 triplet 的 anchor,positive 和 negative 样本均属于同一个 group。ERNet 为每一个 group 学习得到一个 γ 维的桥上道路描述子(属于该 group 的桥上训练样本的 ERNet 的特征 embedding 的均值)和 γ 维的桥下道路描述子。本文γ被设置为 10。
此外,考虑到卷积神经网络的参数共享机制的成功,研究者对 SPP 特征也使用了参数共享机制。具体地,每个六边形的输入 SPP 特征(12 维)单独通过 3 个全连接层(w1、w2 和 w3)。19 个六边形的 SPP 特征共享相同的 w1、w2 和 w3。SPP 的参数共享不仅能够带来更高的性能,同样能够极大的降低计算代价,详见对比实验部分。
置信度约束
对于一个 group G,ERNet 学习一个γ维的桥上道路描述子 A 和桥下道路描述子 B,见下图 13。在预测阶段,对于一个属于 G 的位置,ERNet 预测得到一个γ维的特征 embedding C。如果 ||A-C||<||B-C||,该位置可以被识别为位于高架道路桥上。否则,位置可以被识别为在桥下。尽管这样做,ERNet 已经能够取得较高的准确率,但是对于工业级别的应用而言,准确率仍然略有不足。
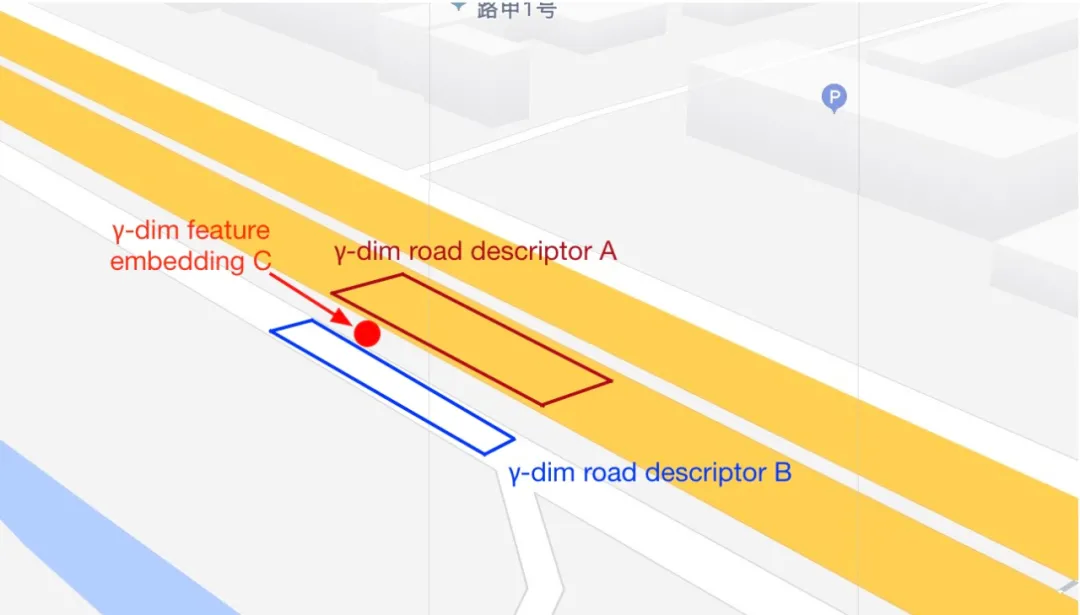
图 13:ERNet 为每个 group 学习桥上道路描述子 A 和桥下道路描述子 B。预测阶段,ERNet 为每个位置预测特征 embedding C。
因此,研究者提出使用 confidence constraint(置信度约束技术)提供 ERNet 的预测准确率(98.6% 到 99.2%,详见实验部分)。具体地,在训练集中,他们为每一个样本的预测结果计算 confidence:
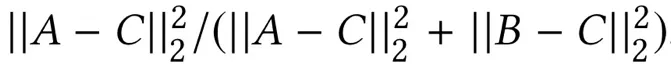
置信度等于 0(或 1)表示该位置更像是在高架桥上(或高架桥下)。在一个 group 中,我们将预测结果进行排序。在每一个预测的 confidence c 上,计算
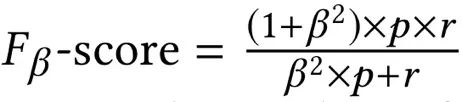
这里 p = L / M,r = L / N。N 是类别为高架桥上的样本个数,M 是 confidence 小于 c 的样本的个数,L 是 M 中类别为高架桥上的样本个数。β是用来平衡 p 和 r 的值。β越小,表示越看重准确率。本文中,研究者设置β为 0.25,因为希望准确率更高些。
对应最大 F_β - score 的置信度值即为 group G 的桥上约束值 Ve。在推断阶段,只有样本的置信度小于 Ve,样本才能被识别为桥上。类似地,group G 也有一个桥下约束值 Vs。在推断阶段,只有样本的置信度大于 Vs,样本才能被识别为桥下。如果样本即不能识别为桥上,也不能识别为桥下,那么样本被认为是未知状态。
下图 14 是对置信度约束的一个形象描述。所谓置信度约束,可以认为是为桥上的道路描述子和桥下的道路描述子各加了一个置信度半径。对于桥上样本而言,样本的特征 embedding 不仅需要到桥上的描述子更近,而且需要在桥上描述子的置信度半径内。
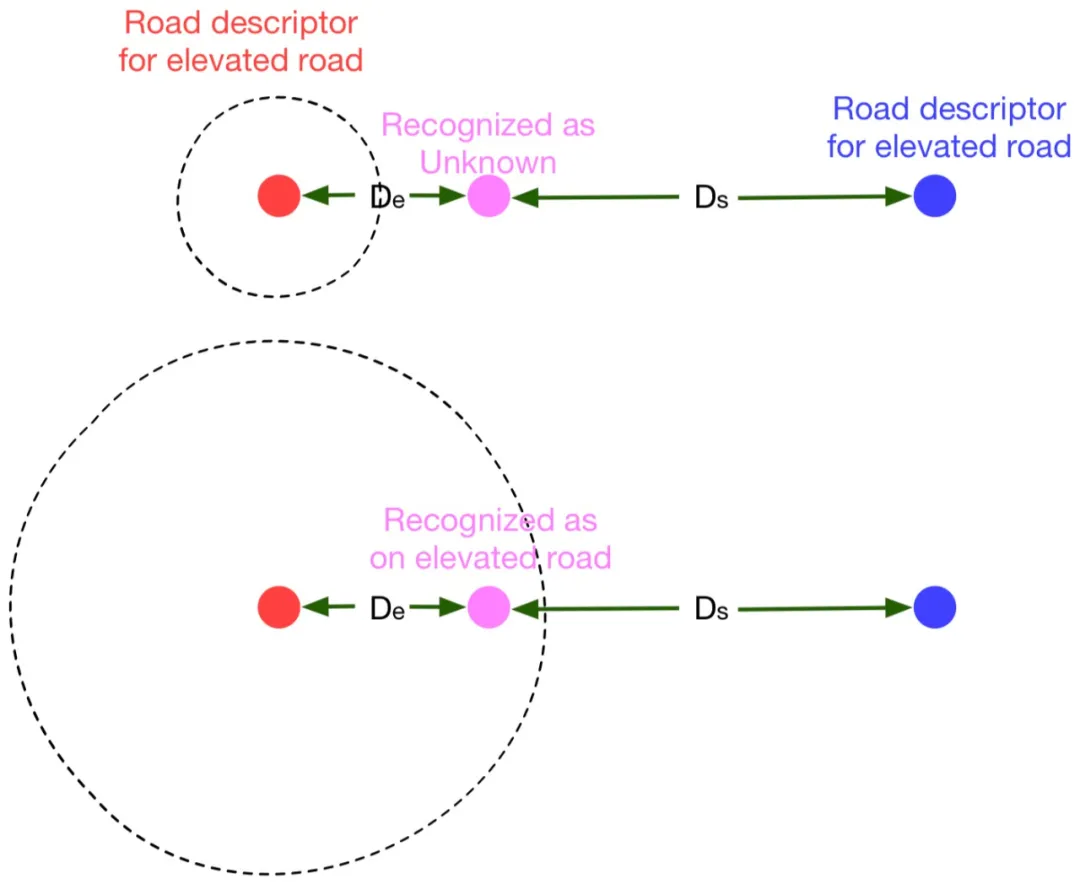
图 14:置信度约束可以被视为在道路描述子外侧加上置信度半径。一个位置被识别为在桥上,不仅需要该位置的特征 embedding 距离桥上道路描述子更近,而且需要在桥上道路描述子的置信度半径内。
基于 ERNet 的偏航检测方法
研究者基于 ERNet,研究者提出了一个新的偏航检测方法。该检测方法运行在手机端。在导航过程中,ERNet 会不断地预测车辆当前的状态(行驶在高架桥上还是桥下)。在一个没有重叠的 k 秒的时间窗口内,如果车辆规划行驶在桥上 / 桥下,而 ERNet 连续识别车辆行驶在桥下 / 桥上,一个偏航事件即可被检测出来。
下图 15 是一个偏航检测的示例:车辆规划行驶在高架桥上,但是车辆实际行驶在高架桥下的平行辅路。ERNet 连续识别出车辆行驶在桥下,因此一次偏航事件即可以被检测出来。
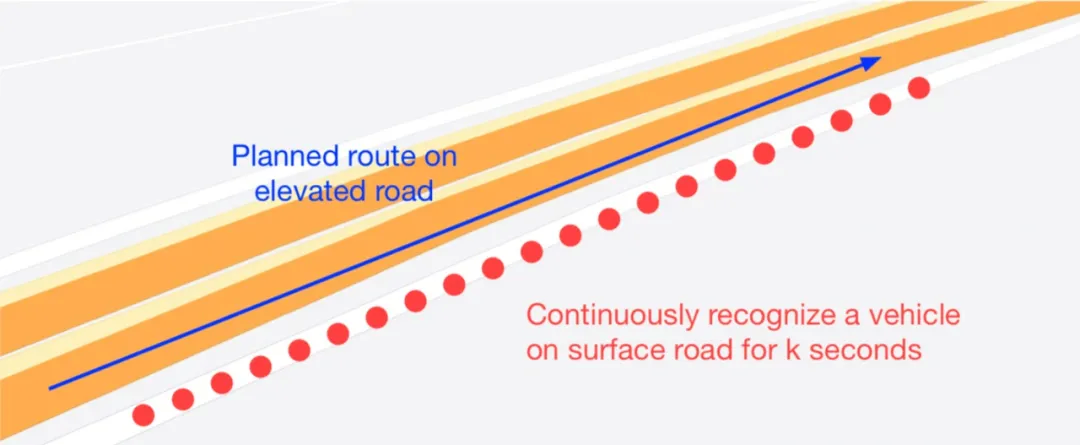
图 15:规划路线为桥上时,ERNet 连续(k 秒)识别车辆行驶在桥下,一次偏航事件被检测出。
实验
研究者在北京、上海和广州三个城市,测试了高架道路网络在高架道路识别和偏航检测两个任务上的效果。下图 16 为北上广三个城市高架区域(绿色矩形框内)。
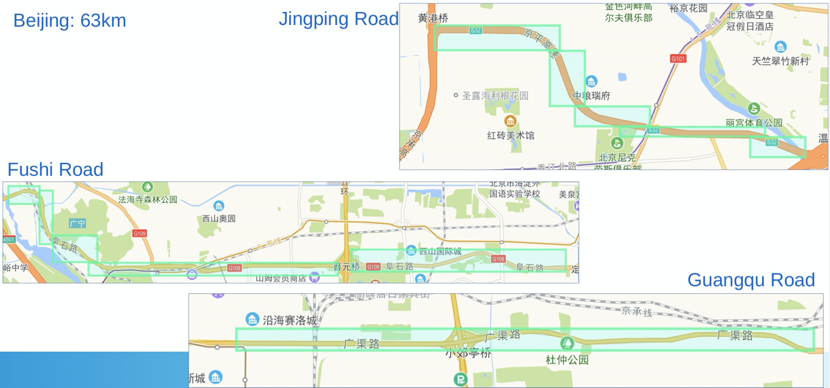
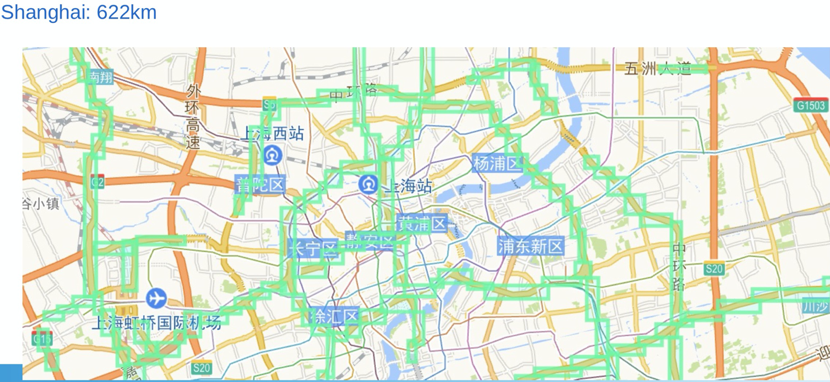
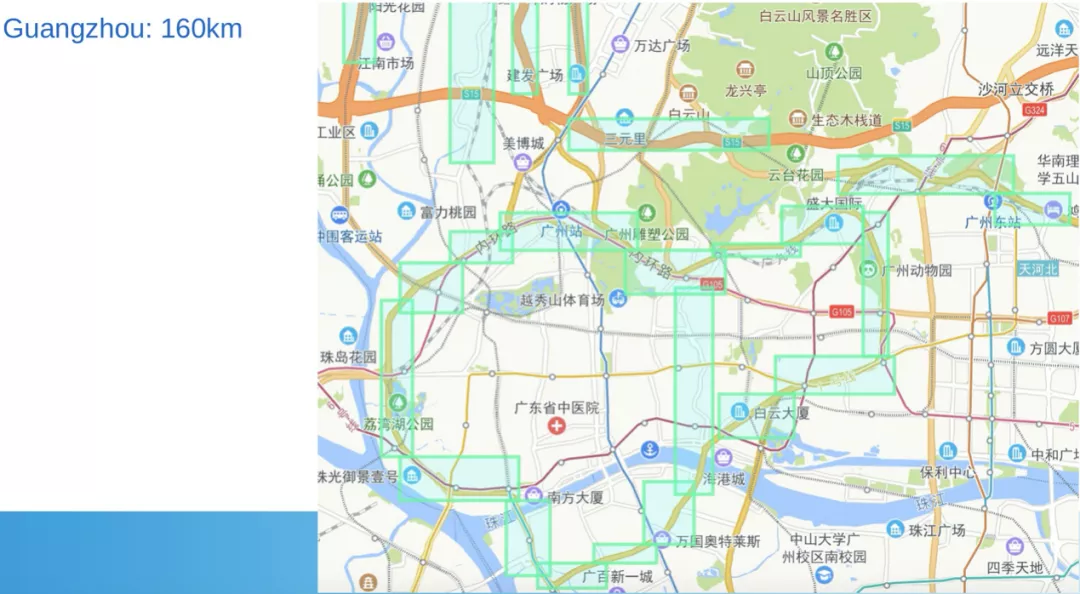
图 16:北京、上海、广州三个城市的高架桥区分布。
数据集
由于暂无公开的数据集,因此研究者在 Android 手机上搜集数据,构造本文的训练数据集和测试数据集。对于 iPhone 手机,无法获取到卫星的底层信号(如卫星的空间位置和信噪比等),因此 本文方法只针对 Android 手机适用 。
训练数据集
研究者使用一个非常大的训练数据集。该数据集的类别是自动标注的,存在大约 3% 的标注类别噪声。自动标注算法总共标注了数十亿个样本(每个样本对应一个位置)。对于每一个 group,研究者只采样最多 4000 个样本用于训练。当然,如果一个 group 的样本仅包含桥上或桥下类别,则会舍弃该 group。训练数据总共包含约一亿个样本。
测试数据集
研究者的测试数据集按照轨迹组织。 70% 的轨迹用作评估集,30% 用作验证集 。每个实例包含:A)SPP 特征、高架道路距离、group ID 和序列速度特征;B)道路标注类别(高架桥上 / 高架桥下);C)经度、纬度、高度、速度和运动方向;D)规划道路类别(规划行驶桥上 / 规划行驶桥下)。A、B、和 C 用来评估特征识别方法和匹配识别方法。D 用来评估偏航检测方法。
为了构造测试数据集,研究者同样搜集 Android 手机的 GNSS 和规划路线数据,跟构造训练集类似。但是,为了确保真值的准确性,研究者手动标注车辆行驶的道路。标注参考车辆行驶的速度、交通信号灯、路网拓扑等信息。尽管标注也会存在一些误标注数据,但总体上要更为可靠些。
由于北京、上海和广州三个城市的高架道路长度分别是 63km、622km 和 160km,因此测试数据集的轨迹在三个城市的分布为 1:10:3。如果一条轨迹包含标注道路类别和规划路线道路类别不一致的位置,则称该轨迹为偏航轨迹。
评估协议
对于高架道路识别任务,其目标为识别为车辆是否在高架桥上行驶。研究者定义识别准确率 p=T / (T + F)和识别有效率 r=(T+F) / (T + F + U)。T 为正确识别的位置个数,F 为错误识别的位置个数,U 为识别为未知状态的数量。下图 17 中对应的 p=10 / 12,r = 12 / 14。
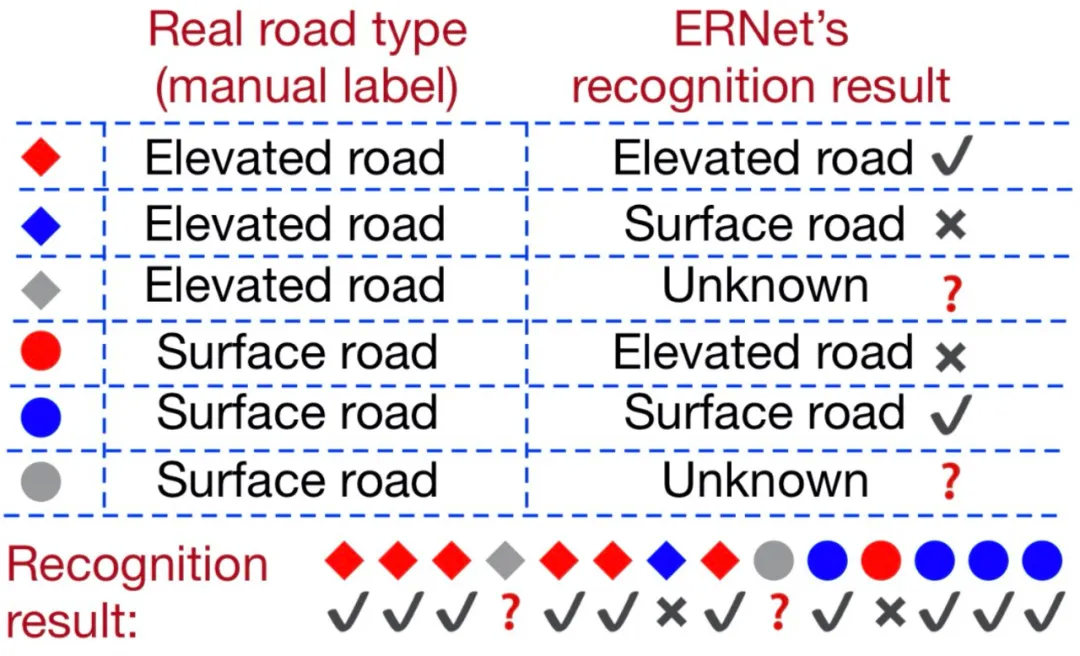
图 17:14 个位置中,10 个位置被正确识别,12 个位置存在识别结果。
对于偏航检测,研究者考虑偏航准确率 yaw_p 和偏航召回率 yaw_r。其中 yaw_p 为正确偏航的次数除以总共偏航的次数,yaw_r 为正确偏航的轨迹数除以偏航轨迹的数量(注意,一条轨迹仅偏航一次,因为线上实际应用时,偏航后会立即重新规划路线)。
参数实验
ERNet 有三个超参数:α、β和γ。α代表 group 的长度,β代表序列速度的 bin 数量,γ代表道路描述子的大小。基于 ERNet 的偏航检测方法有一个超参数:k,表示无重叠时间窗口的大小。在验证测试集上,经过多组参数对比实验,如下图 18,研究者选择了最优的参数组合α=20,β=35,γ=10,k=15。
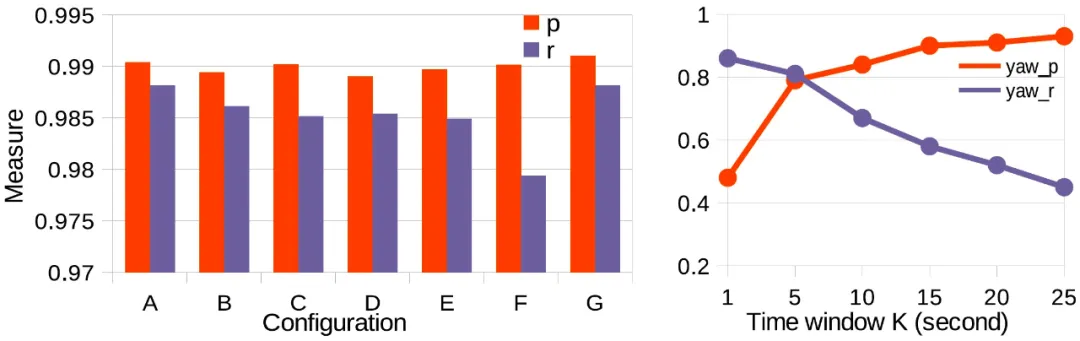
图 18:(a)α、β和γ在 A:20、35、10,在 B:10、35、10,在 C:40、35、10,在 D:20、20、10,在 E:20、50、10,在 F:20、35、5,在 G:20、35、20;(b)我们设置 k 为 1、5、10、15、20、25。
高架状态识别实验结果
研究者用如下方法对比 ERNet 在高架状态识别的实验结果:
GNSS-rule 和 DEEL 是论文 [2] 提出的方法,在论文 [2] 的私有数据集上进行评估。该数据集仅包含 4 个 Android 手机在上海的数据。Bar-rule 是研究者实现的一个基于气压计的方法,其在他们私有的 iPhone 数据集上进行评估。其余的方法均在评估测试集上进行评估。
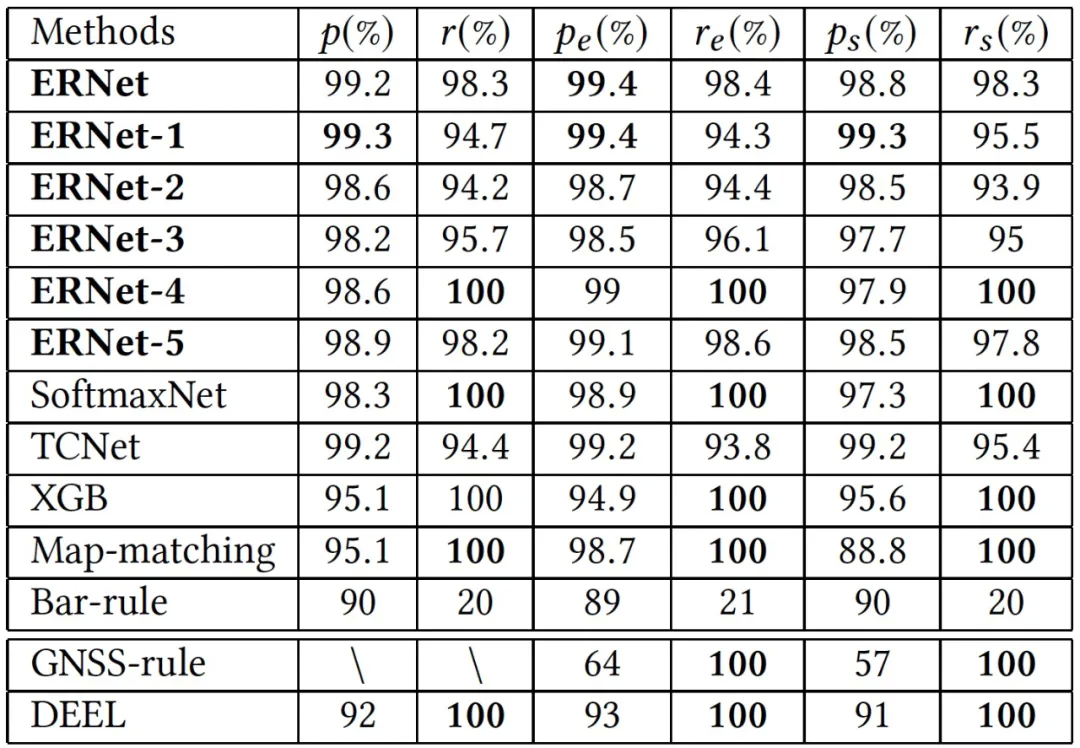
表 1:高架道路识别的对比方法实验结果。
表 1 显示 ERNet 获得了最优的效果。对比 ERNet-1,ERNet 的 r 提升了 3.6%,而 p 仅降低了 0.1%,这证明了 group ID 的有效性。对比 ERNet-2,ERNet 的 r 提升 4.1%,p 提升 0.6%,同样证明了 SPP 特征的有效性。对比 ERNet-3,ERNet 的 r 提升了 2.6%,p 提升了 1%,序列速度特征同样很重要。
不使用置信度约束时,ERNet-4 的 r 是 100%,但是 p 为 98.6%。不过研究者更希望准确率能够有足够大的提升,因此置信度约束也是有必要的。对比 ERNet-5,ERNet 的 SPP 特征的共享机制不仅轻微提升了 p 和 r,而且 ERNet’的计算代价仅为 ERNet-5 的 1/5。
研究者比较 ERNet-4 和 SoftmaxNet,可以发现使用 triplet loss 训练使得 p 略微增加 0.3%。不过对于桥下样本的 p 增加为 0.6%。因此 triplet loss 的引入也是有一定价值的,能够体现出高架道路识别局部问题的属性。TCNet 的效果较差,这值得进一步的讨论分析。
至于其余的对比方法,效果明显弱于 ERNet 和 ERNet 的变种。下图 19 显示了 ERNet 在 10 款流行手机和 3 个城市的实验效果。可以看出,ERNet 对于不同机型和不同城市的性能比较稳定。注意横轴的刻度是非常细的。
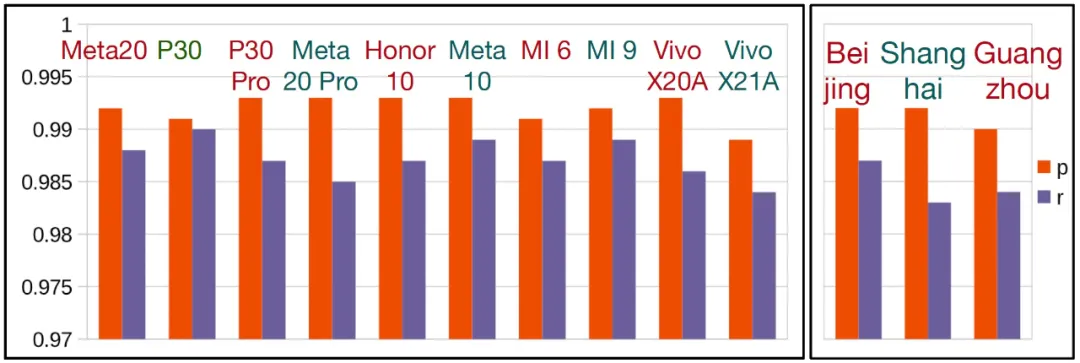
图 19:ERNet 在 10 款流行手机(左子图)和 3 个城市(右子图)的实验结果。
下图 20 展示了两个识别例子。图 20(a)是一个 good-case。ERNet 的识别结果是非常好的,即使在入口处;而图 20(b)则是一个 bad-case。车辆从高架区域外的道路驶入高架区域,中间没有经过入口。按照常识,此处应该全部识别为高架桥下。但是 ERNet 并没有考虑道路的拓扑关系(道路的联通性、出入口等),后续可以考虑引入道路的拓扑关系解决这类 bad-case。
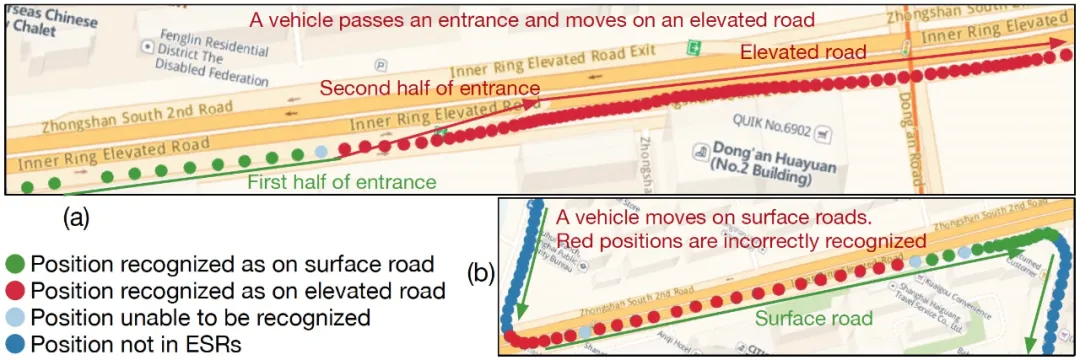
图 20:(a)ERNet 输出稳定的识别结果,即使在入口处;(b)Bad-cases 也许可以通过引入道路拓扑关系解决(此处没有入口,因此车辆不可能在高架桥上行驶)。
T-SNE 可视化
卫星信号特征的特征空间非常巨大,因此较难学习到区分度非常强的特征表示(76 维的卫星信号表示,SPP 参数共享的最后一层),下如图 21(a)。而结合其它三类特征后,学习得到的道路描述子的可分度非常强,如图 21(b)。
此外,高架道路识别是一个局部问题,ERNet 在学习过程中不要求属于不同 group 的同类样本距离彼此非常近,而只要求同一个 group 内的同类样本在特征空间上靠近彼此,如图 21(c)。
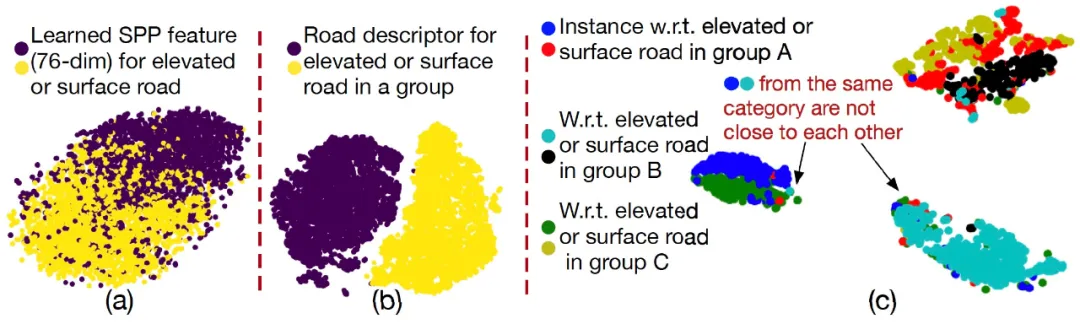
图 21:单独依靠 SPP 特征,无法学习足够区分度的特征(a)。而结合其余三类特征后,ERNet 能够学习出足够区分度的道路描述子(b)和特征 embedding(c)。
偏航检测实验结果
研究者对比基于气压计的偏航检测方法和传统的偏航检测方法(高德线上偏航算法)。气压计的偏航检测方法容易受车辆开窗关窗影响(车窗打开后,车辆速度较快的情况下,气压计读数会在短时间内降低,对应测量的高度短时间内增加)。
下表 2 显示基于 ERNet 的偏航检测方法在准确率和召回率上都远超基于气压计的偏航检测方法。需要注意的是,传统的偏航检测方法无法检测出高架场景的偏航事件。

表 2:在评估测试集上的偏航检测结果。
未来展望
在本文中,研究者提出了 ERNet,一个轻量级而且真正工业级的模型,使用 triplet loss 进行训练,从根本上解决高架道路识别问题。
在未来,研究者会将 ERNet 扩展到全国。并探索如何使用道路拓扑信息降低误识别。此外,现在的偏航检测方法至少需要 15 秒才能识别出车辆偏航。这对于用户的体验并不是最佳的。因此,研究者考虑使用循环神经网络对偏航检测方法进行建模,期望能够在更短时间检测出偏航。
引文
[1] Tianqi Chen and Carlos Guestrin. 2016. XGBoost: A Scalable Tree Boosting System. In KDD. 785–794.
[2] Yaoming Gong, Yanmin Zhu, and Jiadi Yu. 2015. DEEL: Detecting Elevation of Urban Roads with Smartphones on Wheels. In IEEE International Conference on Sensing, Communication, and Networking.
[3] GPS Accuracy 2017. GPS.GPS Overview 2017. GPS.Xinwei He, Yang Zhou, Zhichao Zhou, Song Bai, and Xiang Bai. 2018. Triplet-Center Loss for Multi-View 3D Object Retrieval. In CVPR. 1945–1954.
[6] Alexander Hermans, Lucas Beyer, and Bastian Leibe. 2017. In Defense of the Triplet Loss for Person Re-Identification. In arXiv.
[7] Ping-Fan Ho, Chia-Che Hsu, Jyh-Cheng Chen, and Tao Zhang. 2018. Poster: Using Barometer on Smartphones to Improve GPS Navigation Altitude Accuracy. In MobiCom. 741–743.
[8] Diederik P Kingma and Jimmy Ba. 2015. Adam: A Method for Stochastic Optimization. In ICLR.
[9] Yin Lou, Chengyang Zhang, Xing Xie, Yu Zheng, Wei Wang, and Yan Huang. 2009. Map-Matching for Low-Sampling-Rate GPS Trajectories. In SIGSPATIAL.
[10] Paul E Newson and John Krumm. 2009. Hidden Markov map matching through noise and sparseness. In International Conference on Advances in Geographic Information Systems. 336–343.
[11] Florian Schroff, Dmitry Kalenichenko, and James Philbin. 2015. FaceNet: A unified embedding for face recognition and clustering. In CVPR. 815–823.
[12] Xiaocheng Tang, Zhiwei Qin, Fan Zhang, Zhaodong Wang, Zhe Xu, Yintai Ma, Hongtu Zhu, and Jieping Ye. 2019. A Deep Value-network Based Approach for Multi-Driver Order Dispatching. In KDD. 1780–1790.
[13] Yandong Wen, Kaipeng Zhang, Zhifeng Li, and Yu Qiao. 2016. A Discriminative Feature Learning Approach for Deep Face Recognition. In ECCV. 499–515.
[14] Can Yang and Gyozo Gidofalvi. 2018. Fast map matching, an algorithm integrating hidden Markov model with precomputation. International Journal of Geographical Information Science 32, 3 (2018), 547–570.
[15] Yu Zheng. 2015. Trajectory>
原文链接 :
手机端上线,破解高架区域偏航检测难题,高德提出工业级轻量模型ERNet