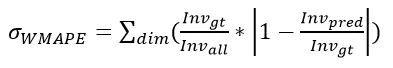
背景
广告仍然是互联网流量变现及商业模式的重要手段,随着互联网高速的发展,广告服务愈加精细化,需要提前预知用户的访问量来保证广告的策略,这就需要理解和预测广告库存量,这就是广告库存预估。广告库存预估属于时间序列预测任务,主要利用历史库存来预测未来一天或多天的广告库存,从而预估出更为准确的库存,对广告售前询量、离线分配等工作有极为重要的指导作用。
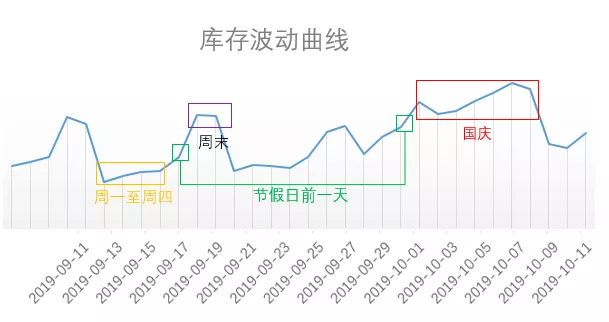
广告库存预估作为时间序列预测算法的业务场景之一,其数据拥有时间序列数据的基本特点,趋势性与随机性并存,在长期的规律性中蕴含了短期的波动性;同时,广告库存预估有以下几个业务特点和难点:
解决方案
1.1 常用方案
时序预测方法主要可以分为两种方法: 传统时序建模方法和机器学习。
最初的传统时序预测,可以追溯到移动平均法、指数平滑法,这类方法基于某段时间的历史数据拟合曲线,对于周期性的波动或方差较大的数据模拟效果较差;之后,随着移动平均与自回归的 ARMA,ARIMA 等模型出现,时序预测与此相结合。ARIMA 模型[1],全称差分整合移动平均自回归模型,其中 AR 是自回归,I 为整合,MA 为滑动平均,模型主要采用三个参数分别表示时序数据的滞后数、达到稳定状态需要的差分阶数、预测误差的滞后数。[1] 该模型简单易实现,对近期数据波动规律捕捉较好。但是 ARIMA 模型要求观测数据本身或是其差分后的数据是稳定的,且模型重点关注内生变量,不易添加外部特征,尤其与时序关联较小的特征。
随着人工智能的发展,机器学习方法开始普及,SVM、XGBoost 等方法也被运用于时序预测任务中。深度学习作为机器学习中的一种被不断提及,其中,循环神经网络 RNN 逐渐被证明在时序预测中能获得较好的效果,在捕捉长期数据规律上更有不错的表现。
在调研 LSTM 算法模型之前,爱奇艺广告算法团队采用 Adaptive-ARIMA 模型(后文简称为 A-ARIMA 模型),进行广告库存预估。A-ARIMA 模型将传统 ARIMA 算法和库存预估背景相结合,主要流程如下:
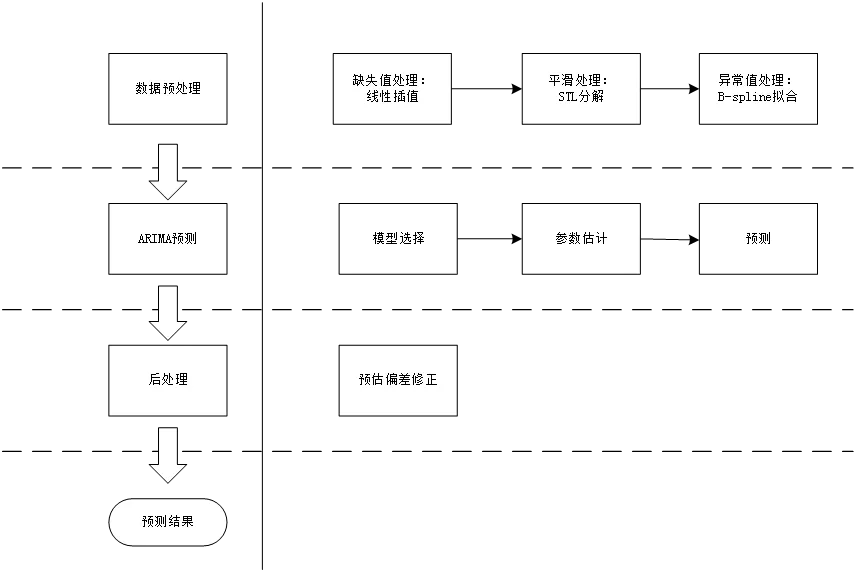
其中,A-ARIMA 算法对于传统 ARIMA 的改进主要在于缺失值、异常值等处理,另外,在后续处理时加入了进出节假日及周末的预估偏差矫正,以更好地描述实际流量波动。实验结果显示:在库存预估场景下,A-ARIMA 模型较传统算法预测效果更好,偏差率下降 1.16pp。
1.2 基于 LSTM 模型的预估算法
LSTM(Long short-term memory,长短期记忆)模型[2],属于 RNN(Recurrent neural network,循环神经网络)模型的一种,在长序列预测过程中相比普通 RNN 有更好的效果。在确定采用 LSTM 模型作为基础网络模型后,需要构建基本数据集:以过去 N 天的历史库存数据作为训练集,设置时间滑动窗口为 t,则每个维度每 t 天的数据可作为一个训练样本,而随后的一天数据则作为标签值,同时,为了保证参数训练方向的随机性,在选择训练样本时,我们采用随机选取样本的方式,而不是将单一维度的样本依次放入训练。LSTM 整体网络结构如下:
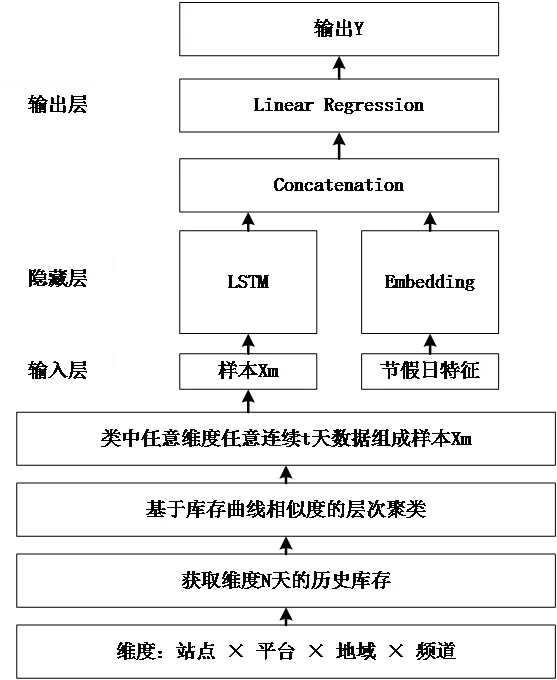
该结构基于 LSTM 网络模型主要有以下几个优化点:
数据归一化是机器学习中的常见方法,在此进行归一化的主要原因是为了使得不同样本能训练同一组模型参数。具体针对这一问题,库存预估在不同维度下库存量级差距巨大,热门维度库存量可达到近千万,而部分维度则只有个位数的库存,而且同一维度下也可能存在库存水平随时间区间的变化而大幅浮动的情况。因此,在数据输入至 LSTM 网络前,需要对数据进行归一化。
我们分析了对数函数转换、min-max 标准化、z-score 标准化、最大值标准化等不同的归一化方法,发现最大值标准化在归一化效果和预测效果上都更加稳定。值得注意的是,相对于 min-max 方法在归一化时扣减训练数据最小值从而改变数据偏移量,直接采用最大值标准化能避免改变时序数据的相关性。最大值标准化方法具体可描述为:设一个维度可被划分为 M 个 RNN 样本,其中第 m 个样本为
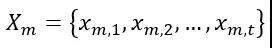
对应 label 为
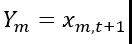
则归一化后的样本数据可表示为
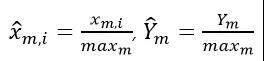
其中
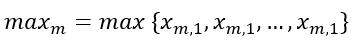
正如库存预估业务特点中所描述,预估维度通常需要精确到站点、平台、城市、频道等维度。若对各维度采用相同参数的 LSTM 网络,模型则很难准确地描述各个维度;反之,如果每一个维度单独训练,样本数不够,模型将失去泛化性,且训练成本过大。
本文希望通过聚类的方法,选择波动趋势近似的维度组成同一类,进而训练相同的模型参数,因此,首先需计算 IAE 误差并完成层次聚类[3],组成所需数据集。
IAE(Integrated AbsoluteError) ,综合绝对误差,公式表示为:
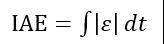
t 为时间周期,表示某时刻两条库存曲线之间的误差,由于实际问题中库存值不连续,体现为离散的点,故该公式可表示为:
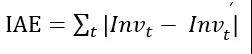
从几何角度分析,该误差公式可理解为两条库存曲线相交部分的面积大小,以此表示维度之间的“距离”。得到各维度两两之间的“距离”后,可利用该结果进行聚类,聚类过程可视为将库存曲线波动趋势相似的维度放入同一类。
下图展示了两个类的聚类效果:
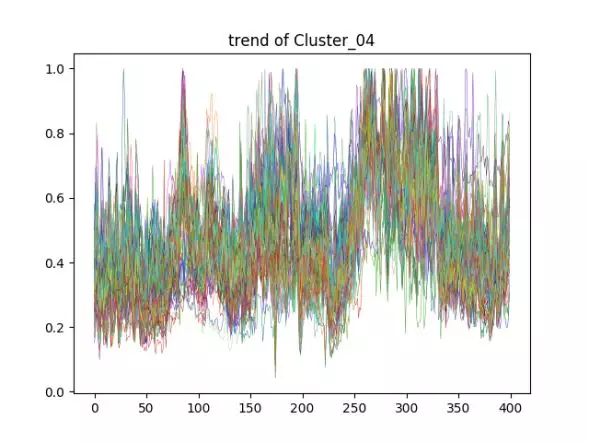
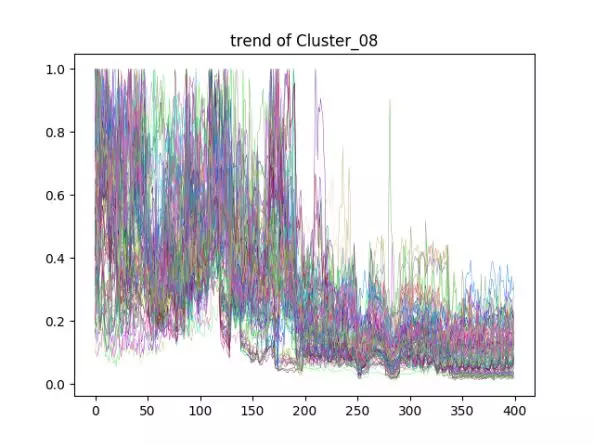
可以明显看出,这两类间的各个维度曲线整体波动趋势差异明显,而同一类内的曲线波动趋势比较近似。因此,根据聚类结果,对不同类训练不同参数的 LSTM 模型能更好地描述各维度库存波动趋势,而且这也不需要占用过多的训练资源。
实验结果
通过上述方案构建基于 LSTM 模型的库存预估方法后,我们需要对模型的准确性进行评估。本文的主要比较对象为 LSTM 模型单天预估结果和 A-ARIMA 模型预估结果,采用来自 2019 年 6、7、8、9 四个月,共 49 天的数据,包含了暑假期间及暑假前后,同时每星期的数据包含了工作日与周末,样本具有较好的代表性与随机性。评估指标采用加权偏差率,描述如下:
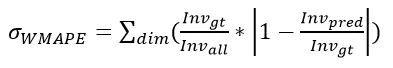
实验数据表明:在维度加权偏差率方面,LSTM 模型相较于 A-ARIMA 模型整体日均下降 0.72pp。而在全维度总库存预估上, LSTM 预测偏差率日均下降 1.48pp,效果更为明显。基于以上实验结果,我们可以判断基于 LSTM 的广告库存预估算法较 A-ARIMA 算法有更好的预测效果。
总结与展望
将 LSTM 模型运用于广告库存预估的背景下,通过比对 A-ARIMA 模型与 LSTM 模型的预测结果,实验数据表明 LSTM 模型在广告库存预估上具有更高的准确度。为了更好地适应业务特点,主要在以下几个方面进行优化:
基于 LSTM 预估模型的模型,广告库存预估深度学习算法取得了较好的预估结果。在未来的工作中,会不断的优化和探索更加准确有效的方法,如构建更准确的节假日特征,更准确地捕捉到库存波动曲线的特征等,将不断提升广告库存预估结果的精确度。